
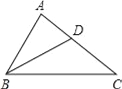
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.
【答案】(1)33°;(2)证明见解析.(3)证明见解析.
【解析】试题分析:(1)在BC上截取BE=AB,利用“边角边”证明△ABD和△BED全等,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证;
(2)由(1)知:△ABD≌△BED,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,等量代换得到EC=AD,即得答案BC=BE+EC=AB+AD;
(3)为了把∠A=2∠C转化成两个角相等的条件,可以构造辅助线:在AC上取BF=BA,连接AE,根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F.再根据勾股定理表示出BC2,AB2.再运用代数中的公式进行计算就可证明.
试题解析:(1)在BC上截取BE=BA,如图1,
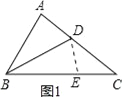
在△ABD和△BED中,
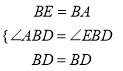 ,
,
∴△ABD≌△BED,
∴∠BED=∠A,
∵∠C=38°,∠A=2∠C,
∴∠A=76°,
∴∠ABC=180°﹣∠C﹣∠A=66°,
BD平分∠ABC,
∴∠ABD=33°;
(2)由(1)知:△ABD≌△BED,
∴BE=AB,DE=AD,∠BED=∠A,
又∵∠A=2∠C,
∴∠BED=∠C+∠EDC=2∠C,
∴∠EDC=∠C,
∴ED=EC,
∴EC=AD
∴BC=BE+EC=AB+AD;t
(3)如图2,过B作BG⊥AC于G,
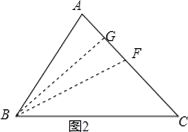
以B为圆心,BA长为半径画弧,交AC于F,
则BF=BA,
在Rt△ABG和Rt△GBG中,
![]() ,
,
∴Rt△ABG≌Rt△GBG,
∴AG=FG,
∴∠BFA=∠A,
∵∠A=2∠C,
∴∠BFA=∠FBC+∠C=2∠C,
∴∠FBC=∠C,
∴FB=FC,
FC=AB,
在Rt△ABG和Rt△BCG中,
BC2=BG2+CG2,
AB2=BG2+AG2
∴BC2﹣AB2=CG2﹣AG2=(CG+AG)(CG﹣AG)
=AC(CG﹣GF)=ACFC
=ACAB.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠ABO=45°,∠CDO=90°,∠COD=60°)
(1)如图1摆放,点O、A、C在一直线上,则∠BOD的度数是多少?
(2)如图2,将直角三角板OCD绕点O逆时针方向转动,若要OB恰好平分∠COD,则∠AOC的度数是多少?
(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( ) 
A.4+4﹣ ![]() =6
=6
B.4+40+40=6
C.4+ ![]() =6
=6
D.4﹣1÷ ![]() +4=6
+4=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA= ![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.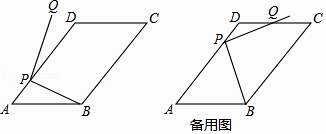
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题: ①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1 , 四边形DABE的面积为S2 , 则S1=S2 ,
那么( )
A.①是真命题②是假命题
B.①是假命题②是真命题
C.①是假命题②是假命题
D.①是真命题②是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
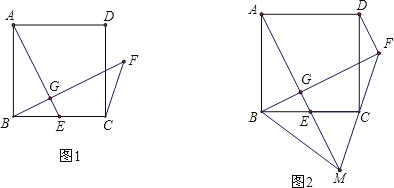
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、M、B、N、C在同一直线上顺次排列,点M是线段AB的中点,点N是线段MC的中点,点N在点B的右边.
![]()
(1)填空:图中共有线段 条;
(2)若AB=6,MC=7,求线段BN的长;
(3)若AB=a,MC=7,将线段BN的长用含a的代数式表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P. 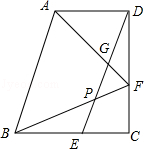
(1)求证:AB=BF;
(2)如果BE=2EC,求证:DG=GE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com