
����Ŀ����֪��һ�����ǰ壨ֱ�����ǰ�OAB��ֱ�����ǰ�OCD����AOB=90�㣬��ABO=45�㣬��CDO=90�㣬��COD=60�㣩
��1����ͼ1�ڷţ���O��A��C��һֱ���ϣ����BOD�Ķ����Ƕ��٣�
��2����ͼ2����ֱ�����ǰ�OCD�Ƶ�O��ʱ�뷽��ת������ҪOBǡ��ƽ�֡�COD�����AOC�Ķ����Ƕ��٣�
��3����ͼ3�������ǰ�OCD�ڷ��ڡ�AOB�ڲ�ʱ��������OMƽ�֡�AOC������ONƽ�֡�BOD��������ǰ�OCD�ڡ�AOB���Ƶ�O����ת������MON�Ķ����Ƿ����仯��������䣬����ֵ������仯��˵�����ɣ�

���𰸡���1��30�㣻(2) 60�㣻(3) ����75��
��������
�������ǰ�ǵ������ͽ�ƽ���ߵĶ�����
��1��������ǵĶ��弴�ɵõ����ۣ�
��2���ɽ�ƽ���ߵĶ���õ���BOC=![]() ��COD=
��COD=![]() ��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��3�����ݽ�ƽ���ߵĶ���õ�![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
�⣺��1��![]() ��
��
��2����BOC=![]() ��COD=
��COD=![]() ��60��=30�㣬
��60��=30�㣬
���AOC=��AOB����BOC=90�㩁30��=60�㣻
��3����BOD+��AOC=90�㩁��COD=90�㩁60��=30�㣬
![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15�㣬
��30��=15�㣬
��MON=![]() ����BOD+��AOC��+��COD=15��+60��=75��
����BOD+��AOC��+��COD=15��+60��=75��
����MON�Ķ������ᷢ���仯������75�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��չ��������д���������Ϊ�˽�ѧ���IJ���������ڸ�У�����ȡ���ĸ��༶ѧ�����е��飬���ռ����������������Ƴ�ͼ1��ͼ2�����в�������ͳ��ͼ�������ͼ�е���Ϣ������������⣺ 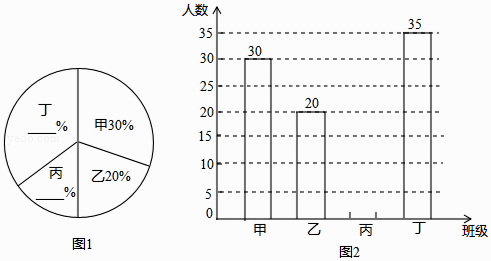
��1�����ĸ�����������ѧ�����ˣ�
��2�����㲹ȫ����ͳ��ͼ��
��3����ͼ1�мװ�����Ӧ������Բ�ĽǵĶ�����
��4�����ĸ��༶��ѧ��������160�ˣ�ȫУ��2000�ˣ��������ȫУ��ѧ���в�����λ�Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУѧ����ѧ�ڲμ������Ĺ滮��������������ѧУ��������˱�У50��ѧ���μ�������Ĵ����������������õ������������£�
�μ������������Ƶ����Ƶ��
�����x | Ƶ�� | Ƶ�� |
0��x��3 | 10 | 0.20 |
3��x��6 | a | 0.24 |
6��x��9 | 16 | 0.32 |
9��x��12 | 6 | 0.12 |
12��x��15 | b | m |
15��x��18 | 2 | n |
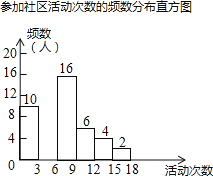
��������ͼ����Ϣ������������⣺
��1������a= �� b= �� m= �� n= .
��2�����Ƶ���ֲ�ֱ��ͼ������������ͼ�����ע��Ӧ�����ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����Rt��ACB�У���ACB=90�㣬��D��AB���е㣬��E��CD���е㣬����C��CF��AB��AE���ӳ����ڵ�F�� 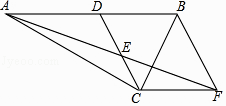
��1����֤����ADE�ա�FCE��
��2������DCF=120�㣬DE=2����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ���±���ʾ�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ��ͼ��ʾ��
ʱ��t���죩 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
�������� | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
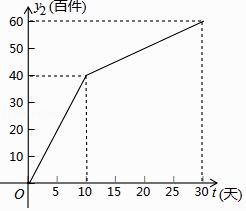
��1��������һ�κ��������κ����ͷ����������У�ѡ����ʵĺ����ܷ�ӳy1��t�ı仯���ɣ������y1��t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��2����y2��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڸ��ٵ����30���У���ʵ���̵�������̵������������Ϊy���ټ�������y��t�ĺ�����ϵʽ����tΪ��ֵʱ������������y�ﵽ��������ʱ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�EΪBC�ߵ��е㣬CD��AB��AB=2��AC=1��DE= ![]() �����CDE+��ACD=�� ��
�����CDE+��ACD=�� �� 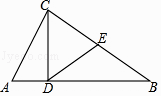
A.60��
B.75��
C.90��
D.105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=k1x-3(k1��0)��ͼ����x�ᡢy��ֱ���A��B���㣬
�뷴��������y=![]() (k2��0)��ͼ����C,D���㣬��CE��y�ᣬ����Ϊ��E����DF��y�ᣬ����Ϊ��F����֪CE=1��
(k2��0)��ͼ����C,D���㣬��CE��y�ᣬ����Ϊ��E����DF��y�ᣬ����Ϊ��F����֪CE=1��
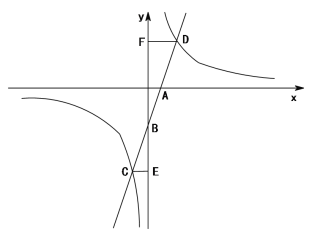
(1) ��ֱ��д����C������ (��k1����ʾ)
��k2��k1=�� ����
(2) ��BΪAC���е㣬���������ı���ʽ��
(3) ��(2)�������£����M��x�Ḻ������һ�㣬���߶�MF�Ƶ�M��˳ʱ�����ʱ�뷽����ת90���õ��߶�MN������M����ʱ����N�ܷ��ڷ�����������ͼ���ϣ�����ܣ������N�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������2400�ף��ס������˷ֱ��A��B����ͬʱ����������У��ҵ��ٶ��Ǽ�2������֪�ҵ���A��15���Ӻ����B�أ�
��1�����ÿ�����߶����ף�
��2�����˳������ٷ��Ӻ�ǡ�����480�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
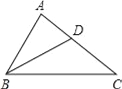
����Ŀ����ͼ������ABC�У�BDƽ�֡�ABC����A=2��C��
��1������C=38�������ABD=��������������
��2����֤��BC=AB+AD��
��3����֤��BC2=AB2+ABAC��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com