
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P. 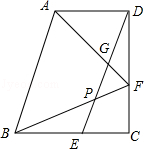
(1)求证:AB=BF;
(2)如果BE=2EC,求证:DG=GE.
【答案】
(1)证明:∵BC=CD,BE=DF,
∴CF=CE,
在△BCF与△DCE中,
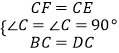 ,
,
∴△BCF≌△DCE,
∴BF=DE,
∵AD∥BC,BE=AD,
∴四边形ABED是平行四边形;
∴AB=DE,
∴AB=BF
(2)证明:延长AF交BC延长线于点M,则CM=CF;
∵AD∥BC,
∴ ![]() =
= ![]() ,
,
∵BE=2EC,
∴ ![]() =
= ![]() =1,
=1,
∴DG=GE.
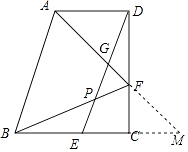
【解析】(1)先证△BCF≌△DCE,再证四边形ABED是平行四边形,从而得AB=DE=BF.(2)延长AF交BC延长线于点M,从而CM=CF,又由AD∥BC可以得到 ![]() =
= ![]() =1,从而DG=GE.
=1,从而DG=GE.
【考点精析】认真审题,首先需要了解直角梯形(一腰垂直于底的梯形是直角梯形),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
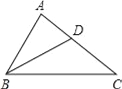
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅客携带x kg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量x kg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量x kg的对应关系


(1) 如果旅客选择托运,求可携带的免费行李的最大重量为多少kg?
(2) 如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量x kg之间的函数关系式
(3) 某旅客携带25kg的行李,设托运m kg行李(10≤m<24,m为正整数),剩下的行李选择快递.当m为何值时,总费用y的值最小?并求出其最小值是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:

(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
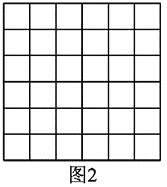
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF.
的格点△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为_______,CD的长为______,AD的长为________;
(3)四边形ABCD的面积为________.
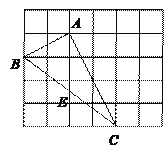
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的圆柱形容器的容积为81升,它的底面直径是高的2倍.(π取3)
(1)这个圆柱形容器的底面直径为多少分米?
(2)若这个圆柱形容器的两个底面与侧面都是用铁皮制作的,则制作这个圆柱形容器需要铁皮多少平方分米?(不计损耗)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;
②AD与AC互相垂直;
③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;
⑤线段AB是B点到AC的距离.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( )
(x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( ) 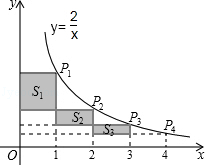
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com