
【题目】某旅客携带x kg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量x kg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量x kg的对应关系


(1) 如果旅客选择托运,求可携带的免费行李的最大重量为多少kg?
(2) 如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量x kg之间的函数关系式
(3) 某旅客携带25kg的行李,设托运m kg行李(10≤m<24,m为正整数),剩下的行李选择快递.当m为何值时,总费用y的值最小?并求出其最小值是多少元?
【答案】(1)可携带的免费行李的最大质量为20公斤.(2)快递费y2(元)与行李质量x(公斤)的函数关系式为y2= .(3)当托运20公斤、快递5公斤行李时,总费用最少,最少费用为22元.
.(3)当托运20公斤、快递5公斤行李时,总费用最少,最少费用为22元.
【解析】(1)观察图象找出两点的坐标,利用待定系数法可求出托运费y1(元)与行李质量x(公斤)的函数关系式,将y1=0代入函数关系式中即可得出结论;
(2)根据表格中的数据,分x=1、1<x≤5、5<x≤15三部分找出快递费y2(元)与行李质量x(公斤)的函数关系式;
(3)分10≤m<20以及20≤m<24两种情况找出y关于m的函数关系式,根据一次函数的性质可找出y的取值范围,找出当y取最小值时m的值即可得出结论.
(1)设托运费y1(元)与行李质量x(公斤)的函数关系式为y1=kx+b,
将(30,300)、(50,900)代入y1=kx+b,
![]() ,解得:
,解得:![]() ,
,
∴托运费y1(元)与行李质量x(公斤)的函数关系式为y1=30x-600.
当y1=30x-600=0时,x=20.
答:可携带的免费行李的最大质量为20公斤.
(2)根据题意得:当x=1时,y2=10;
当1<x≤5时,y2=10+3(x-1)=3x+7;
当5<x≤15时,y2=10+3×(5-1)+5(x-5)=5x-3.
综上所述:快递费y2(元)与行李质量x(公斤)的函数关系式为y2=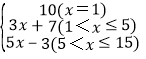 .
.
(3)当10≤m<20时,5<25-m≤15,
∴y=y1+y2=0+5×(25-m)-3=-5m+122.
∵10≤m<20,
∴22<y≤72;
当20≤m<24时,1<25-m≤5,
∴y=y1+y2=30m-600+3×(25-m)+7=27m-518.
∵20≤m<24,
∴22≤y<130.
综上可知:当m=20时,总费用y的值最小,最小值为22.
答:当托运20公斤、快递5公斤行李时,总费用最少,最少费用为22元.


科目:初中数学 来源: 题型:
【题目】如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( ) 
A.4+4﹣ ![]() =6
=6
B.4+40+40=6
C.4+ ![]() =6
=6
D.4﹣1÷ ![]() +4=6
+4=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、M、B、N、C在同一直线上顺次排列,点M是线段AB的中点,点N是线段MC的中点,点N在点B的右边.
![]()
(1)填空:图中共有线段 条;
(2)若AB=6,MC=7,求线段BN的长;
(3)若AB=a,MC=7,将线段BN的长用含a的代数式表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() ,
, ![]() ,试说明:BE∥CF.
,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:
解:∵ ![]() (已知)
(已知)
∴AE∥ ( )
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
∴DC∥AB( )
∴![]() ( )
( )
即![]()
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴BE∥CF( ) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点 A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离等于19,那么n的值是__.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC与∠BOC的平分线OM、ON.
(1)在图1中,射线OC在∠AOB的内部.
①若锐角∠BOC=30°,则∠MON= °;
②若锐角∠BOC=n°,则∠MON= °.
(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.
(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P. 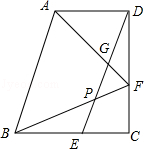
(1)求证:AB=BF;
(2)如果BE=2EC,求证:DG=GE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
(1)如图,在平面内有不共线的3个点A,B,C.
(a)作直线AB,射线AC,线段BC;
(b)延长BC到点D,使CD=BC,连接AD;
(c)作线段AB的中点E,连接CE;
(d)测量线段CE和AD的长度,直接写出二者之间的数量关系_______.

(2) 有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
注意:只需添加一个符合要求的正方形,并用阴影表示.
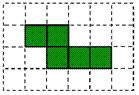
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com