
【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA= ![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.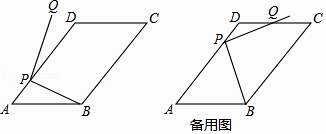
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)
【答案】
(1)
解:如图1中,

①当点Q在平行四边形ABCD内时,∠AP′B=180°﹣∠Q′P′B﹣∠Q′P′D=180°﹣90°﹣10°=80°,
②当点Q在平行四边形ABCD外时,∠APB=180°﹣(∠QPB﹣∠QPD)=180°﹣(90°﹣10°)=100°,
综上所述,当∠DPQ=10°时,∠APB的值为80°或100°
(2)
解:如图2中,连接BQ,作PE⊥AB于E.
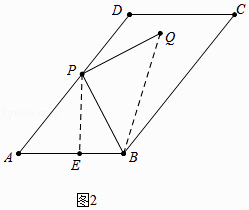
∵tan∠ABP:tanA=3:2,tanA= ![]() ,
,
∴tan∠ABP=2,
在Rt△APE中,tanA= ![]() =
= ![]() ,设PE=4k,则AE=3k,
,设PE=4k,则AE=3k,
在Rt△PBE中,tan∠ABP= ![]() =2,
=2,
∴EB=2k,
∴AB=5k=10,
∴k=2,
∴PE=8,EB=4,
∴PB= ![]() =4
=4 ![]() ,
,
∵△BPQ是等腰直角三角形,
∴BQ= ![]() PB=4
PB=4 ![]()
(3)
解:①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F.则四边形BEPF是矩形.
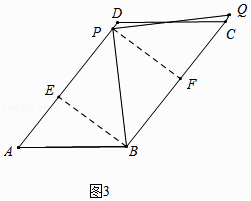
在Rt△AEB中,∵tanA= ![]() =
= ![]() ,∵AB=10,
,∵AB=10,
∴BE=8,AE=6,
∴PF=BE=8,
∵△BPQ是等腰直角三角形,PF⊥BQ,
∴PF=BF=FQ=8,
∴PB=PQ=8 ![]() ,
,
∴PB旋转到PQ所扫过的面积= ![]() =32π.
=32π.
②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F.设PE=x.
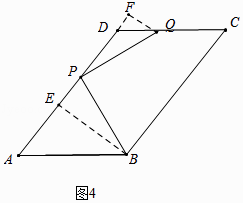
易证△PBE≌△QPF,
∴PE=QF=x,EB=PF=8,
∴DF=AE+PE+PF﹣AD=x﹣1,
∵CD∥AB,
∴∠FDQ=∠A,
∴tan∠FDQ=tanA= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x=4,
∴PE=4, ![]() =4
=4 ![]() ,
,
在Rt△PEB中,PB=, ![]() =4
=4 ![]() ,
,
∴PB旋转到PQ所扫过的面积= ![]() =20π
=20π
③如图5中,
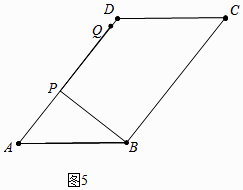
当点Q落在AD上时,易知PB=PQ=8,
∴PB旋转到PQ所扫过的面积= ![]() =16π,
=16π,
综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π
【解析】(1)分两种情形①当点Q在平行四边形ABCD内时,②当点Q在平行四边形ABCD外时,分别求解即可;(2)如图2中,连接BQ,作PE⊥AB于E.在Rt△APE中,tanA= ![]() =
= ![]() ,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP=
,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP= ![]() =2,推出EB=2k,推出AB=5k=10,可得k=2,由此即可解决问题;(3)分三种情形分别求解即可;
=2,推出EB=2k,推出AB=5k=10,可得k=2,由此即可解决问题;(3)分三种情形分别求解即可;
【考点精析】通过灵活运用平行四边形的性质和解直角三角形,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F. 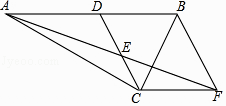
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距2400米,甲、乙两人分别从A,B两地同时出发相向而行,乙的速度是甲的2倍,已知乙到达A地15分钟后甲到达B地.
(1)求甲每分钟走多少米?
(2)两人出发多少分钟后恰好相距480米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)为了迎接新年的到来,学校准备向每位同学赠送一张贺年卡,甲、乙两家都可以印制这种贺年卡,甲厂要收制版费600元,且印制每张0.35元,乙厂要收制版费500元,且印制每张0.40元,两厂制作的贺年卡的质量一样.
①当印制多少张时,甲、乙两厂的收费一样?
②如果要印制2500张,选择哪一家合算?
③根据你的计算和判断,你认为印制多少张时,选择甲厂更合算?印制多少张时,选择乙厂更合算?
(2)我校每天中午总是在规定时间打开学校大门,七年级新生小明每天中午同一时间从家骑自行车到学校,星期一中午他以每小时15千米的速度到校,结果在校门口等了6分钟才开门,星期二中午他以每小时9千米的速度到校,结果校门刚好已开了6分钟,星期三中午小明想准时到达学校门口,那么小明骑自行车的速度应该为每小时多少千米?
根据下面思路,请完成此题的解答过程:
解:设星期三中午小明从家骑自行车准时到达学校门口所用时间为t小时,则星期一中午小明从家骑自行车到达学校门口所用时间为 小时,星期二中午小明从家骑自行车到达学校门口所用时间为 小时,由题意列方程得:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 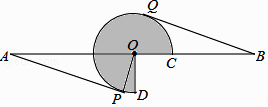
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
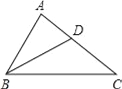
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
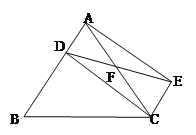
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:

(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
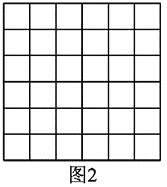
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF.
的格点△DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com