
ЁОЬтФПЁПдкЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЌDЮЊABБпЕФжаЕуЃЌвдDЮЊжБНЧЖЅЕуЕФRtЁїDEFЕФСэСНИіЖЅЕуEЃЌFЗжБ№ТфдкБпACЃЌCBЃЈЛђЫќУЧЕФбгГЄЯпЃЉЩЯЃЎ
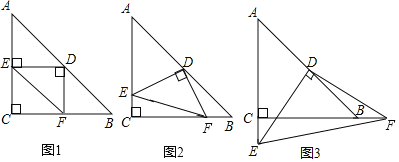
ЃЈ1ЃЉШчЭМ1ЃЌШєRtЁїDEFЕФСНЬѕжБНЧБпDEЃЌDFгыЁїABCЕФСНЬѕжБНЧБпACЃЌBCЛЅЯрДЙжБЃЌдђSЁїDEF+SЁїCEFЃН![]() SЁїABCЃЌЧѓЕБSЁїDEFЃНSЁїCEFЃН2ЪБЃЌACБпЕФГЄЃЛ
SЁїABCЃЌЧѓЕБSЁїDEFЃНSЁїCEFЃН2ЪБЃЌACБпЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєRtЁїDEFЕФСНЬѕжБНЧБпDEЃЌDFгыЁїABCЕФСНЬѕжБНЧБпACЃЌBCВЛДЙжБЃЌSЁїDEF+SЁїCEFЃН![]() SЁїABCЃЌЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіSЁїDEFЃЌSЁїCEFЃЌSЁїABCжЎМфЕФЪ§СПЙиЯЕЃЛ
SЁїABCЃЌЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіSЁїDEFЃЌSЁїCEFЃЌSЁїABCжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєRtЁїDEFЕФСНЬѕжБНЧБпDEЃЌDFгыЁїABCЕФСНЬѕжБНЧБпACЃЌBCВЛДЙжБЃЌЧвЕуEдкACЕФбгГЄЯпЩЯЃЌЕуFдкCBЕФбгГЄЯпЩЯЃЌSЁїDEF+SЁїCEFЃН![]() SЁїABCЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіSЁїDEFЃЌSЁїCEFЃЌSЁїABCжЎМфЕФЪ§СПЙиЯЕЃЎ
SЁїABCЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіSЁїDEFЃЌSЁїCEFЃЌSЁїABCжЎМфЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЛЃЈ2ЃЉГЩСЂЃЌРэгЩЯъМћНтЮіЃЛЃЈ3ЃЉВЛГЩСЂЃЌSЁїDEFЉSЁїCEFЃН![]() SЁїABCЃЎ
SЁїABCЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїDEЪЧЁїABCЕФжаЮЛЯпЃЌЕУГіDE![]() BCЃЌACЃН2CEЃЌЭЌРэDFЃН
BCЃЌACЃН2CEЃЌЭЌРэDFЃН![]() ACЃЌжЄГіЫФБпаЮDECFЪЧе§ЗНаЮЃЌЕУГіCEЃНDFЃНCFЃНDEЃЌЕУГіSЁїDEFЃНSЁїCEFЃН2ЃН
ACЃЌжЄГіЫФБпаЮDECFЪЧе§ЗНаЮЃЌЕУГіCEЃНDFЃНCFЃНDEЃЌЕУГіSЁїDEFЃНSЁїCEFЃН2ЃН![]() DEDFЃН
DEDFЃН![]() DF2ЃЌЧѓГіDFЃН2ЃЌМДПЩЕУГіACЃН2CEЃН4ЃЛ
DF2ЃЌЧѓГіDFЃН2ЃЌМДПЩЕУГіACЃН2CEЃН4ЃЛ
ЃЈ2ЃЉСЌНгCDЃЌжЄУїЁїCDEЁеЁїBDFЃЌЕУГіSЁїCDEЃНSЁїBDFЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉВЛГЩСЂЃЛСЌНгCDЃЌЭЌЃЈ2ЃЉЕУГіЁїDECЁеЁїDBFЃЌЕУГіSЁїDEFЃНSЮхБпаЮDBFECЃНSЁїCFE+SЁїDBCЃНSЁїCFE+![]() SЁїABCЃЎ
SЁїABCЃЎ
НтЃКЃЈ1ЃЉЁпЁЯACBЃН90ЁуЃЌDEЁЭACЃЌDFЁЭBCЃЌ
ЁрЫФБпаЮDECFЪЧОиаЮЃЌ
ЁпЁЯACBЃН90ЁуЃЌ
ЁрBCЁЭACЃЌ
ЁпDEЁЭACЃЌ
ЁрDEЁЮBCЃЌ
ЁпDЮЊABБпЕФжаЕуЃЌ
ЁрDEЪЧЁїABCЕФжаЮЛЯпЃЌ
ЁрDEЃН![]() BCЃЌACЃН2CEЃЌ
BCЃЌACЃН2CEЃЌ
ЭЌРэЃКDFЃН![]() ACЃЌ
ACЃЌ
ЁпACЃНBCЃЌ
ЁрDEЃНDFЃЌ
ЁрЫФБпаЮDECFЪЧе§ЗНаЮЃЌ
ЁрCEЃНDFЃНCFЃНDEЃЌ
ЁпSЁїDEFЃНSЁїCEFЃН2ЃН![]() DEDFЃН
DEDFЃН![]() DF2ЃЌ
DF2ЃЌ
ЁрDFЃН2ЃЌ
ЁрCEЃН2ЃЌ
ЁрACЃН2CEЃН4ЃЛ
ЃЈ2ЃЉSЁїDEF+SЁїCEFЃН![]() SЁїABCГЩСЂЃЌРэгЩШчЯТЃК
SЁїABCГЩСЂЃЌРэгЩШчЯТЃК
СЌНгCDЃЛШчЭМ2ЫљЪОЃК
ЁпACЃНBCЃЌЁЯACBЃН90ЁуЃЌDЮЊABжаЕуЃЌ
ЁрЁЯBЃН45ЁуЃЌЁЯDCEЃН![]() ЁЯACBЃН45ЁуЃЌCDЁЭABЃЌCDЃН
ЁЯACBЃН45ЁуЃЌCDЁЭABЃЌCDЃН![]() ABЃНBDЃЌ
ABЃНBDЃЌ
ЁрЁЯDCEЃНЁЯBЃЌЁЯCDBЃН90ЁуЃЌSЁїABCЃН2SЁїBCDЃЌ
ЁпЁЯEDFЃН90ЁуЃЌ
ЁрЁЯCDEЃНЁЯBDFЃЌ
дкЁїCDEКЭЁїBDFжаЃЌ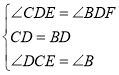 ЃЌ
ЃЌ
ЁрЁїCDEЁеЁїBDFЃЈASAЃЉЃЌ
ЁрDEЃНDFЃЎSЁїCDEЃНSЁїBDFЃЎ
ЁрSЁїDEF+SЁїCEFЃНSЁїCDE+SЁїCDFЃНSЁїBCDЃН![]() SЁїABCЃЛ
SЁїABCЃЛ
ЃЈ3ЃЉВЛГЩСЂЃЛSЁїDEFЉSЁїCEFЃН![]() SЁїABCЃЛРэгЩШчЯТЃК
SЁїABCЃЛРэгЩШчЯТЃК
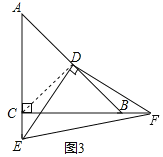
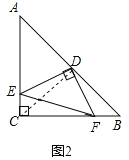
СЌНгCDЃЌШчЭМ3ЫљЪОЃК
ЭЌЃЈ1ЃЉЕУЃКЁїDECЁеЁїDBFЃЌЁЯDCEЃНЁЯDBFЃН135ЁуЃЌ
ЁрSЁїDEFЃНSЮхБпаЮDBFECЃЌ
ЃНSЁїCFE+SЁїDBCЃЌ
ЃНSЁїCFE+![]() SЁїABCЃЌ
SЁїABCЃЌ
ЁрSЁїDEFЉSЁїCFEЃН![]() SЁїABCЃЎ
SЁїABCЃЎ
ЁрSЁїDEFЁЂSЁїCEFЁЂSЁїABCЕФЙиЯЕЪЧЃКSЁїDEFЉSЁїCEFЃН![]() SЁїABCЃЎ
SЁїABCЃЎ


 УћЪІЕуВІОэЯЕСаД№АИ
УћЪІЕуВІОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBACЃН120ЁуЃЌADЦНЗжЁЯBACЃЌЧвADЃНABЃЌШєЁЯEDFЃН60ЁуЃЌЦфСНБпЗжБ№НЛБпABЃЌACгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЪЧЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃКBEЃНAFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧИјГіШчЯТЖЈвхЃКЫГДЮСЌНгШЮвтвЛИіЫФБпаЮИїБпжаЕуЫљЕУЕФЫФБпаЮНажаЕуЫФБпаЮЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЫФБпаЮABCDжаЃЌЕуEЃЌFЃЌGЃЌHЗжБ№ЮЊБпABЃЌBCЃЌCDЃЌDAЕФжаЕуЃЎЧѓжЄЃКжаЕуЫФБпаЮEFGHЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЪЧЫФБпаЮABCDФквЛЕуЃЌЧвТњзуPA=PBЃЌPC=PDЃЌЁЯAPB=ЁЯCPDЃЌЕуEЃЌFЃЌGЃЌHЗжБ№ЮЊБпABЃЌBCЃЌCDЃЌDAЕФжаЕуЃЌВТЯыжаЕуЫФБпаЮEFGHЕФаЮзДЃЌВЂжЄУїФуЕФВТЯыЃЛ
ЃЈ3ЃЉШєИФБфЃЈ2ЃЉжаЕФЬѕМўЃЌЪЙЁЯAPB=ЁЯCPD=90ЁуЃЌЦфЫћЬѕМўВЛБфЃЌжБНгаДГіжаЕуЫФБпаЮEFGHЕФаЮзДЃЎЃЈВЛБижЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ
гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
![]() Шє
Шє![]() ЃЌЪдЫЕУїДЫЗНГЬгаСНИіИКИљЃЎ
ЃЌЪдЫЕУїДЫЗНГЬгаСНИіИКИљЃЎ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌШє
ЕФЬѕМўЯТЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЛГіЁїABCЙигкy жсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіA1ЁЂB1ЁЂC1ЕФзјБъЃЎ
ЃЈ2ЃЉНЋЁїABCЯђгвЦНвЦ6ИіЕЅЮЛЃЌЛГіЦНвЦКѓЕФЁїA2B2C2ЃЛ
ЃЈ3ЃЉЙлВьЁїA1B1C1КЭЁїA2B2C2ЃЌЫќУЧЪЧЗёЙигкФГжБЯпЖдГЦЃПШєЪЧЃЌЧыдкЭМЩЯЛГіетЬѕЖдГЦжсЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]()
(1)ШєЗНГЬгаЪЕЪ§Иљ,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
(2)ШєЗНГЬСНЪЕЪ§ИљЗжБ№ЮЊ![]() ,ЧвТњзу
,ЧвТњзу![]() ,ЧѓЪЕЪ§
,ЧѓЪЕЪ§![]() ЕФжЕЁЃ
ЕФжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
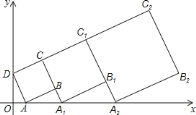
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮ![]() ЕФЮЛжУШчЭМЫљЪОЃЌЕу
ЕФЮЛжУШчЭМЫљЪОЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎбгГЄ
ЃЎбгГЄ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌзїе§ЗНаЮ
ЃЌзїе§ЗНаЮ![]() ЃЛбгГЄ
ЃЛбгГЄ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌзїе§ЗНаЮ
ЃЌзїе§ЗНаЮ![]() ЃЌАДетбљЕФЙцТЩНјааЯТШЅЃЌЕк
ЃЌАДетбљЕФЙцТЩНјааЯТШЅЃЌЕк![]() Иіе§ЗНаЮЃЈе§ЗНаЮ
Иіе§ЗНаЮЃЈе§ЗНаЮ![]() ПДзїЕк
ПДзїЕк![]() ИіЃЉЕФУцЛ§ЮЊЃЈ ЃЉ
ИіЃЉЕФУцЛ§ЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯBAC=90ЁуЃЌЁЯABC=ЁЯACBЃЌгжЁЯBDC=ЁЯBCDЃЌЧвЁЯ1=ЁЯ2ЃЌЧѓЁЯ3ЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
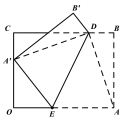
ЁОЬтФПЁПШчЭМЃЌГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌНЋЫФБпаЮ
ЃЌНЋЫФБпаЮ![]() би
би![]() елЕўЃЌШєЕу
елЕўЃЌШєЕу![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЧЁКУТфдкБп
ЧЁКУТфдкБп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ЕФГЄЮЊ____ЃЎ
ЕФГЄЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com