
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,点
,点![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将四边形
,将四边形![]() 沿
沿![]() 折叠,若点
折叠,若点![]() 的对称点
的对称点![]() 恰好落在边
恰好落在边![]() 上,则
上,则![]() 的长为____.
的长为____.
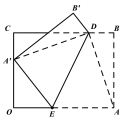
【答案】3.
【解析】
根据矩形的性质得到BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,求得CD=6,BD=2,根据折叠可知A′D=AD,A′E=AE,可证明Rt△A′CD≌Rt△DBA,根据全等三角形的性质得到A′C=BD=2,A′O=4,然后在Rt△A′OE中根据勾股定理列出方程求解即可.
解:如图, 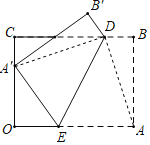
∵四边形OABC是矩形,
∴BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,
∵CD=3DB,
∴CD=6,BD=2,
∴CD=AB,
∵将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,
∴A′D=AD,A′E=AE,
在Rt△A′CD与Rt△DBA中,
![]() ,
,
∴Rt△A′CD≌Rt△DBA(HL),
∴A′C=BD=2,
∴A′O=4,
∵A′O2+OE2=A′E2,
∴42+OE2=(8-OE)2,
∴OE=3,
故答案是:3.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,D为AB边的中点,以D为直角顶点的Rt△DEF的另两个顶点E,F分别落在边AC,CB(或它们的延长线)上.
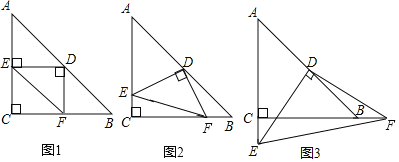
(1)如图1,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC互相垂直,则S△DEF+S△CEF=![]() S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
S△ABC,求当S△DEF=S△CEF=2时,AC边的长;
(2)如图2,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,S△DEF+S△CEF=![]() S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
S△ABC,是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系;
(3)如图3,若Rt△DEF的两条直角边DE,DF与△ABC的两条直角边AC,BC不垂直,且点E在AC的延长线上,点F在CB的延长线上,S△DEF+S△CEF=![]() S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
S△ABC是否成立?若成立,请给予证明;若不成立,请直接写出S△DEF,S△CEF,S△ABC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
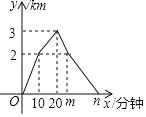
【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在AB、BC、AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
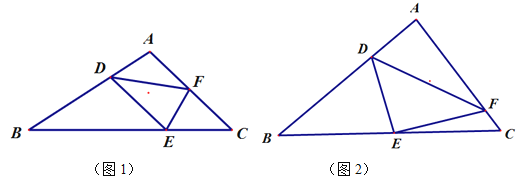
(1)如图1,当DE=DF时,图1中是否存在于AB相等的线段?若存在,请找出并加以证明.若不存在说明理由.
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
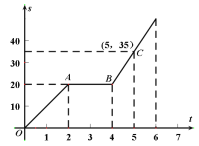
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示:
批发价(元个) | 零售价(元/个) | |
甲型号垃圾桶 | 12 | 16 |
乙型号垃圾桶 | 30 | 36 |
若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,
(1)求y关于x的函数表达式.
(2)若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在四边形ABFC中,![]() =90
=90![]() 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE

(1)试探究,四边形BECF是什么特殊的四边形;
(2)当![]() 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com