
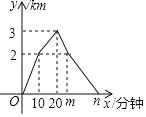
【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?
【答案】(1)25,45;(2)小明回家骑行速度至少是0.3千米/分.
【解析】
(1)根据函数图象,先求出爸爸骑共享单车的速度以及匀速步行的速度,再求出返回途中爸爸从驿站到公园入口的时间,得到m的值;然后求出爸爸从公园入口到家的时间,进而得到n的值;
(2)根据小明要在爸爸到家之前赶上得到不等关系:(n﹣爸爸从驿站到家的时间﹣小明到达驿站后逗留的10分钟)×小明回家骑行的速度≥驿站与家的距离,依此列出不等式,求解即可.
(1)由题意,可得爸爸骑共享单车的速度为:![]() =0.2(千米/分),
=0.2(千米/分),
爸爸匀速步行的速度为:![]() =0.1(千米/分),
=0.1(千米/分),
返回途中爸爸从驿站到公园入口的时间为:![]() =5(分钟),
=5(分钟),
所以m=20+5=25;
爸爸从公园入口到家的时间为:![]() =20(分钟),
=20(分钟),
所以n=25+20=45.
故答案为25,45;
(2)设小明回家骑行速度是x千米/分,
根据题意,得(45﹣25﹣10)x≥3,
解得x≥0.3.
答:小明回家骑行速度至少是0.3千米/分.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
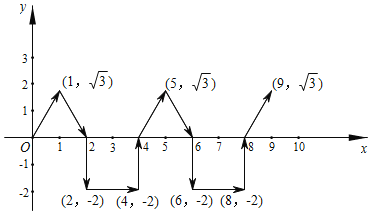
【题目】如图,在平面直角坐标系中,一电子蚂蚁按照设定程序从原点O出发,按图中箭头所示的方向运动,第1次从原点运动到点(1,![]() ),第2次接着运动到点(2,0),第3次接着运动到点(2,﹣2),第4次接着运动到点(4,﹣2),第5次接着运动到点(4,0),第6次接着运动到点(5,
),第2次接着运动到点(2,0),第3次接着运动到点(2,﹣2),第4次接着运动到点(4,﹣2),第5次接着运动到点(4,0),第6次接着运动到点(5,![]() )…按这样的运动规律,经过2019次运动后,电子蚂蚁运动到的位置的坐标是_____.
)…按这样的运动规律,经过2019次运动后,电子蚂蚁运动到的位置的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
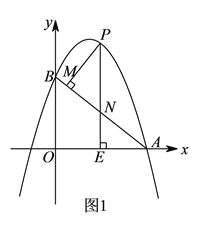
【题目】如图![]() ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(![]() )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
(![]() )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
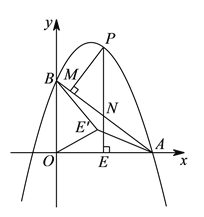
(![]() )如图2,在(
)如图2,在(![]() )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+![]() AE'的最小值.
AE'的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 的边长为 8,E 是 BC 边的中点,点 P 在射线 AD 上, 过 P 作 PF⊥AE 于 F.
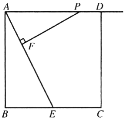
(1)请判断△PFA 与△ABE 是否相似,并说明理由;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶 点的三角形也与△ABE 相似?若存在,请求出 x 的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
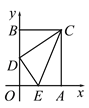
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
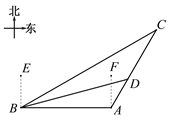
【题目】如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到0.1海里)
≈1.732,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com