
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3a(a≠0)经过点A(﹣1,0).
(1)求抛物线的顶点坐标;(用含a的式子表示)
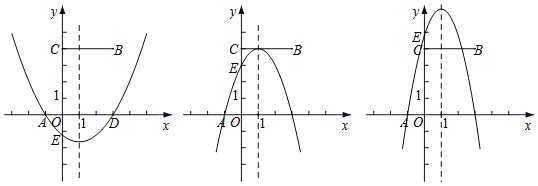
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据抛物线![]() 经过点
经过点![]() 可得a和b的关系,然后将抛物线解析式化为顶点式,即可得到该抛物线的顶点坐标;
可得a和b的关系,然后将抛物线解析式化为顶点式,即可得到该抛物线的顶点坐标;
(2)先根据点坐标平移的变化规律可得点C的坐标,画出当![]() 和
和![]() 时抛物线的图象,然后结合图象即可得到a的取值范围.
时抛物线的图象,然后结合图象即可得到a的取值范围.
(1)∵点![]() 在抛物线
在抛物线![]() 上
上
∴![]() ,解得
,解得![]()
∴![]()
∴抛物线的顶点坐标为![]() ;
;
(2)∵![]()
∴抛物线与x轴的另一个交点坐标为点![]() ,与y轴交于点
,与y轴交于点![]()
∵将点![]() 向左平移3个单位长度
向左平移3个单位长度
![]() 点C的坐标为
点C的坐标为![]() ,即
,即![]()
由题意,分以下两种情况:
①如图,当![]() 时
时
由抛物线与x、y轴的交点可知,抛物线与线段BC无公共点
②当![]() 时
时
若抛物线的顶点在线段BC上,则顶点坐标为![]()
∴![]()
解得![]()
若抛物线的顶点不在线段BC上,要使抛物线与线段BC恰有一个公共点,则抛物线与y轴的交点位于点C的上方
即![]()
解得![]()
综上,a的取值范围是![]() 或
或![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
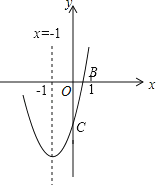
【题目】已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc>0;②2a﹣b=0;③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大:⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan67°≈
,tan67°≈![]() ,sin67°≈
,sin67°≈![]() ,cos67°≈
,cos67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
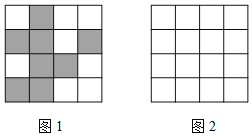
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽同学学习了统计知识后,带领班级“课外活动小组”,随机调查了某辖区若干名居民的年龄,并将调查数据绘制成图①和图②两幅尚不完整的统计图.
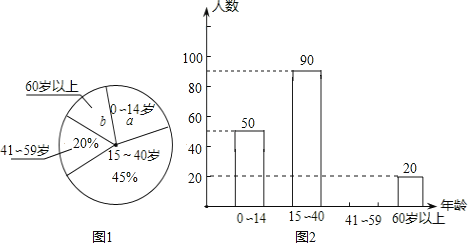
请你根据图中的信息,解答下列各题:
(1)共抽查了_____名居民的年龄,扇形统计图中![]() _____,
_____,![]() ______;
______;
(2)补全条形统计图;
(3)若该辖区居民约有2600人,请你估计年龄在15~59岁的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1,
的正方形网格中,每个小正方形的边长均为1,![]() 的三个顶点均在小正方形的顶点上.
的三个顶点均在小正方形的顶点上.
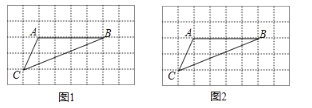
(1)在图1中画一个![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图2中画![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是中心对称图形;
为顶点的四边形是中心对称图形;
(3)直接写出图2中四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
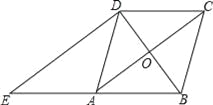
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com