
【题目】小丽同学学习了统计知识后,带领班级“课外活动小组”,随机调查了某辖区若干名居民的年龄,并将调查数据绘制成图①和图②两幅尚不完整的统计图.
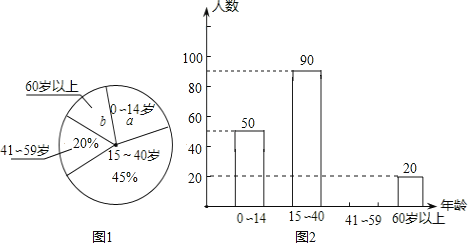
请你根据图中的信息,解答下列各题:
(1)共抽查了_____名居民的年龄,扇形统计图中![]() _____,
_____,![]() ______;
______;
(2)补全条形统计图;
(3)若该辖区居民约有2600人,请你估计年龄在15~59岁的居民人数.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某商场要经营一种文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件.
(1)当每天的利润为1440元时,为了让利给顾客,每件文具的销售价格应定为多少元?
(2)设每天的销售利润为W元,每件文具的销售价格为x元,如果要求每天的销售量不少于10件,且每件文具的利润至少为25元.
①求W与x的函数关系式,并写出自变量的取值范围;
②问当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(白云区校级二模)如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.

(1)连接OD,则OD与AC的位置关系是 .
(2)求AC的长.
(3)求sinE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
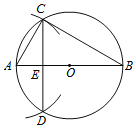
【题目】已知⊙O.如图,
(1)作⊙O的直径AB;
(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
(3)连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3a(a≠0)经过点A(﹣1,0).
(1)求抛物线的顶点坐标;(用含a的式子表示)
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )

A.4B.5C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
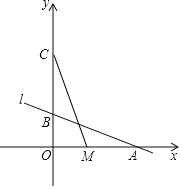
【题目】如图,直线l:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;
(3)设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
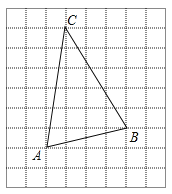
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均落在格点上,
均落在格点上,
(1)![]() 的长等于________;
的长等于________;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
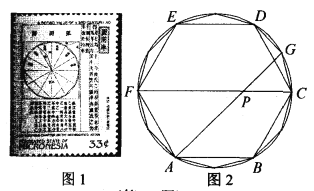
【题目】我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形![]() 是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结
是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com