
����Ŀ��ij�̳�Ҫ��Ӫһ���ľߣ�����Ϊ20Ԫ/������Ӫ���η��֣������ۼ۸�Ϊ25Ԫ/��ʱ��ÿ���������Ϊ250����ÿ�����ۼ۸�ÿ����1Ԫ��ÿ����������ͼ���10����
��1����ÿ�������Ϊ1440Ԫʱ��Ϊ���������˿ͣ�ÿ���ľߵ����ۼ۸�Ӧ��Ϊ����Ԫ��
��2����ÿ�����������ΪWԪ��ÿ���ľߵ����ۼ۸�ΪxԪ�����Ҫ��ÿ���������������10������ÿ���ľߵ���������Ϊ25Ԫ��
����W��x�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
���ʵ����ۼ۸�Ϊ����ʱ�����ľ�ÿ���������������������Ϊ���٣�
���𰸡���1��26Ԫ����2����W����10��x��35��2+2250 ��45��x��49�����ڵ����ۼ۸�Ϊ45Ԫʱ�����ľ�ÿ���������������������Ϊ1250Ԫ��
��������
��1����ÿ���ľߵ����ۼ۸�Ӧ��ΪxԪ��������������������������=���������з������ɵã�
��2���ٸ�����������������������=���������ɵú�������ʽ��
�ڽ���������ʽ�䷽�ɶ���ʽ�������ö��κ������������ɵã�
�⣺��1����ÿ���ľߵ����ۼ۸�Ӧ��ΪxԪ��
�������⣬�ã���x��20��[250��10��x��25��]��1440��
��ã�x1��44��x2��26��
��Ҫ�������˿ͣ�
��x��26��
��ÿ���ľߵ����ۼ۸�Ӧ��Ϊ26Ԫ��
��2��������ã�
W����x��20������10x+500��
����10x2+700x��10000
��![]() ��
��
��45��x��49��
��W����10��x��35��2+2250 ��45��x��49����
��W����10x2+700x��10000
����10��x��35��2+2250��
�ߩ�10��0�������ߵĶԳ���Ϊֱ��x��35
�������߿������£��ڶԳ�����Ҳ࣬W��x���������С
�൱x��45ʱ��Wȡ���ֵΪ1250��
�𣺵����ۼ۸�Ϊ45Ԫʱ�����ľ�ÿ���������������������Ϊ1250Ԫ��


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
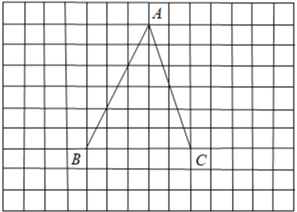
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ![]() �������У�
�������У�![]() ��B��C���ڸ���ϣ�
��B��C���ڸ���ϣ�
����ABC�����Ϊ_______��
��������һ���߳�Ϊ6�������Σ��������AΪ�������ε�һ�����㣬�ҵ�B����C�ֱ��ڸ������ε��������ϣ�������ͼ��ʾ�������У����̶���ֱ�ߣ�������������Σ�����Ҫ˵�����������λ��������ҵ��ģ���Ҫ��֤����___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����
����![]() ��ֱ����
��ֱ����![]() ����
����![]() ���ң�
���ң�![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
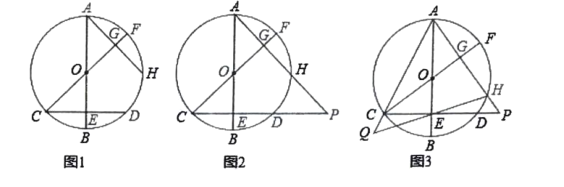
��1����ͼ1����֤��![]() ��
��
��2����ͼ2���ӳ�![]() ���ڵ�
���ڵ�![]() ����֤��
����֤��![]() ��
��
��3����ͼ3���ڣ�2���������£��ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AC��4��BC��3��AB��5��ADΪ��ABC�Ľ�ƽ���ߣ���CD�ij���Ϊ��������

A.1B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����1����x���һ������B������Ϊ��1��0����ͼ����ͼ��ʾ�����н��ۣ���abc��0����2a��b��0����һԪ���η���ax2+bx+c��0���������ǩ�3��1���ܵ�y��0ʱ����3��x��1���ݵ�x��0ʱ��y��x���������������E����4��y1����F����2��y2����M��3��y3���Ǻ���ͼ���ϵ����㣬��y1��y2��y3��������ȷ���У���������
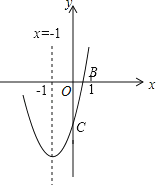
A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
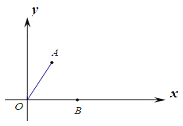
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��![]() ����B��2��0����C����x�����˶�����������ֱ����C�Ĵ��ߣ�����ΪD.����C��x�����˶�ʱ����DҲ��֮�˶������߶�BD�������ֵΪ______________��
����B��2��0����C����x�����˶�����������ֱ����C�Ĵ��ߣ�����ΪD.����C��x�����˶�ʱ����DҲ��֮�˶������߶�BD�������ֵΪ______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������� y��![]() ��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
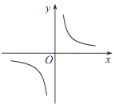
A.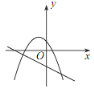 B.
B.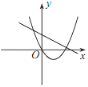 C.
C.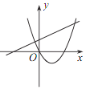 D.
D.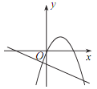
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
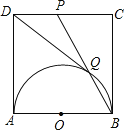
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1����ABΪֱ������Բ����P��CD�е㣬BP���Բ���ڵ�Q������DQ���������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ������______
��������ȷ������______![]() ��д���
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧѧϰ��ͳ��֪ʶ����༶������С�顱�����������ijϽ����������������䣬�����������ݻ��Ƴ�ͼ�ٺ�ͼ�������в�������ͳ��ͼ��
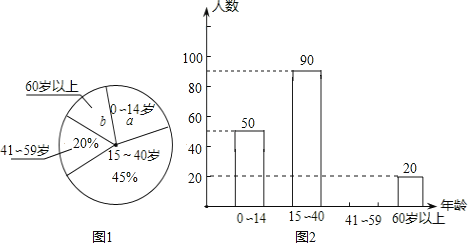
�������ͼ�е���Ϣ��������и��⣺
��1���������_____����������䣬����ͳ��ͼ��![]() _____��
_____��![]() ______��
______��
��2����ȫ����ͳ��ͼ��
��3������Ͻ������Լ��2600�ˣ��������������15��59��ľ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com