
【题目】如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是______
,其中正确结论是______![]() 填写序号
填写序号![]()
【答案】①②④
【解析】
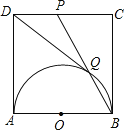
①连接OQ,OD,如图1.易证四边形DOBP是平行四边形,从而可得DO∥BP.结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,则有DQ=DA=1;
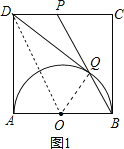
②连接AQ,如图2,根据勾股定理可求出BP.易证Rt△AQB∽Rt△BCP,运用相似三角形的性质可求出BQ,从而求出PQ的值,就可得到![]() 的值;
的值;
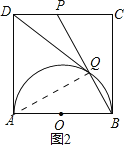
③过点Q作QH⊥DC于H,如图3.易证△PHQ∽△PCB,运用相似三角形的性质可求出QH,从而可求出S△DPQ的值;
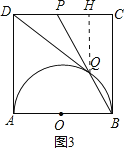
④过点Q作QN⊥AD于N,如图4.易得DP∥NQ∥AB,根据平行线分线段成比例可得![]() ,把AN=1-DN代入,即可求出DN,然后在Rt△DNQ中运用三角函数的定义,就可求出cos∠ADQ的值.
,把AN=1-DN代入,即可求出DN,然后在Rt△DNQ中运用三角函数的定义,就可求出cos∠ADQ的值.
![]() 连接OQ,OD,如图1.
连接OQ,OD,如图1.
易证四边形DOBP是平行四边形,从而可得![]() .
.
结合![]() ,可证到
,可证到![]() ,从而证到
,从而证到![]() ≌
≌![]() ,
,
则有![]() .
.
故![]() 正确;
正确;
![]() 连接AQ,如图2.
连接AQ,如图2.
则有![]() ,
,![]() .
.
易证![]() ∽
∽![]() ,
,
运用相似三角形的性质可求得![]() ,
,
则![]() ,
,
![]() .
.
故![]() 正确;
正确;
![]() 过点Q作
过点Q作![]() 于H,如图3.
于H,如图3.
易证![]() ∽
∽![]() ,
,
运用相似三角形的性质可求得![]() ,
,
![]() .
.
故![]() 错误;
错误;
![]() 过点Q作
过点Q作![]() 于N,如图4.
于N,如图4.
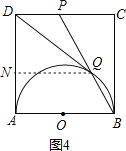
易得![]() ,
,
根据平行线分线段成比例可得![]() ,
,
则有![]() ,
,
解得:![]() .
.
由![]() ,得
,得![]() .
.
故![]() 正确.
正确.
综上所述:正确结论是①②④.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:


(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴下方的抛物线上一动点(包含点
轴下方的抛物线上一动点(包含点![]() ,
,![]() ).作直线
).作直线![]() ,若过点
,若过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)在点![]() 运动的过程中,请求出
运动的过程中,请求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使
,使![]() 是等腰三角形.若存在,请直接写出点
是等腰三角形.若存在,请直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
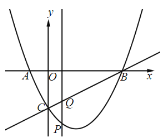
查看答案和解析>>
科目:初中数学 来源: 题型:
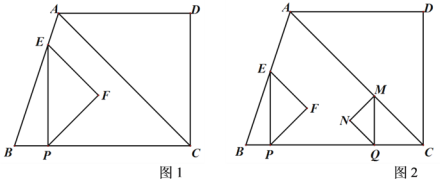
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.
(1)如图1,当∠ADC=90°时,线段MD与ME的数量关系是 ;
(2)如图2,当∠ADC=60°时,试探究线段MD与ME的数量关系,并证明你的结论;
(3)如图3,当∠ADC=α时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=﹣x2+2mx+3m2与x轴相交于点B、C(点B在点C的左侧),与y轴相交于点A,点D为抛物线的顶点,抛物线的对称轴交x轴于点E.
(1)如图1,当AO+BC=7时,求抛物线的解析式;
(2)如图2,点F是抛物线的对称轴右侧一点,连接BF、CF、DF,过点F作FH∥x轴交DE于点H,当∠BFC=∠DFB+∠BFH=90°时,求点H的纵坐标;
(3)如图3,在(1)的条件下,点P是抛物线上一点,点P、点A关于直线DE对称,点Q在线段AP上,过点P作PR⊥AP,连接BQ、QR,满足QB平分∠AQR,tan∠QRP=![]() ,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
,点K在抛物线的对称轴上且在x轴下方,当CK=BQ时,求线段DK的长.
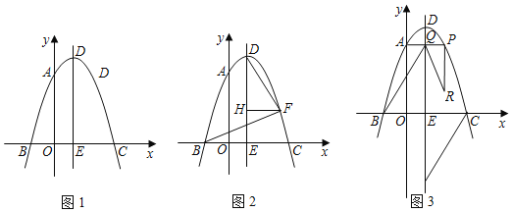
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AC=![]() ,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
(1)当点F恰好落在CD上时,此时t的值为 ;
(2)若P与C重合时运动结束,在整个运动过程中,设等腰直角三角形PEF与四边形ABCD重叠部分的面积为S,请求出S与t之间的函数关系式,并写出自变量t的取值范围;
(3)如图2,在点P开始运动时,BC上另一点Q同时从点C出发,以每秒2个单位长度沿CB方向运动,当Q到达B点时停止运动,同时点P也停止运动,过Q作QM⊥BC交射线CA于点M,以QM为斜边向左作等腰直角三角形QMN,若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一直线上,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com