
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转至
旋转至![]() 的位置,使
的位置,使![]() ,其中点
,其中点![]() 的运动路径为弧
的运动路径为弧![]() ,连接
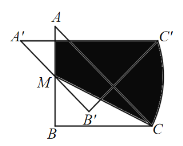
,连接![]() ,则图中阴影部分的面积为_______.
,则图中阴影部分的面积为_______.
【答案】![]() .
.
【解析】
连接MC',由![]() 可证得△A'MH为等腰直角三角形,进而可求得A'H,CH,MH的长,再利用旋转角相等求得∠CMC'的度数,最后利用扇形的面积公式计算即可.
可证得△A'MH为等腰直角三角形,进而可求得A'H,CH,MH的长,再利用旋转角相等求得∠CMC'的度数,最后利用扇形的面积公式计算即可.
解:如图,连接MC',
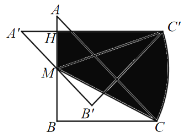
∵在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴∠A=45°,AM=BM=2,AC=![]() ,
,
∵旋转,
∴∠A'=∠A=45°,A'C'=AC=![]() ,A'M=AM=2,
,A'M=AM=2,
又∵![]() ,
,
∴△A'MH为等腰直角三角形,
∴A'H=MH=![]() A'M=
A'M=![]() ,∠A'MH=45°,
,∠A'MH=45°,
∴C'H=A'C'-A'H=![]() ,
,
∴S△MHC'=![]()
在Rt△MHC'中,MC'=![]() ,
,
又∵∠C'MC=∠A'MH=45°,
∴S扇形CMC'=![]() ,
,
∴阴影部分面积为S△MHC'+S扇形CMC'=![]() .
.


科目:初中数学 来源: 题型:
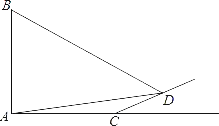
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示,已知每个菱形图案的边长为10![]() cm,其中一个内角为60°.
cm,其中一个内角为60°.
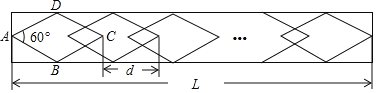
(1)求一个菱形图案水平方向的对角线长;
(2)若d=26,纹饰的长度L能否是6010cm?若能,求出菱形个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块直角三角板如图1放置,等腰直角三角板![]() 的直角顶点是点
的直角顶点是点![]() ,
,![]() ,直角板
,直角板![]() 的直角顶点
的直角顶点![]() 在
在![]() 上,且
上,且![]() ,
,![]() .三角板
.三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]()
![]() .
.
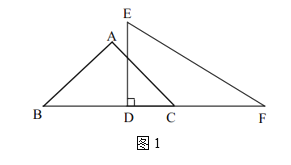
(1)当![]() _______时,
_______时,![]() ;
;
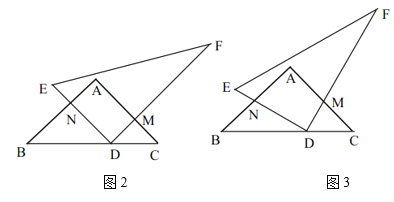
(2)当![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 逆时针旋转至如图2位置,设
逆时针旋转至如图2位置,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)如图3,设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的表达式(不用写
的表达式(不用写![]() 的取值范围).
的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
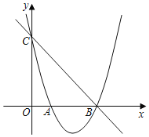
【题目】如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,求PD的长度最大时点P的坐标.
(3)设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
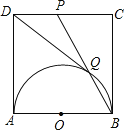
【题目】如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是______
,其中正确结论是______![]() 填写序号
填写序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
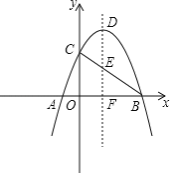
【题目】如图,抛物线![]() 与x轴相交于A、B两点,与y轴交于C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
与x轴相交于A、B两点,与y轴交于C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
(1)求线段DE的长;
(2)设过E的直线与抛物线相交于M(x1,y1),N(x2,y2),试判断当|x1﹣x2|的值最小时,直线MN与x轴的位置关系,并说明理由;
(3)设P为x轴上的一点,∠DAO+∠DPO=∠α,当tan∠α=4时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com