
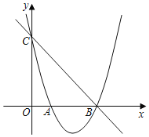
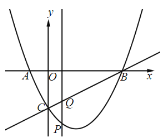
【题目】如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,求PD的长度最大时点P的坐标.
(3)设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)PD的长度最大时点P的坐标为(![]() ,﹣
,﹣![]() );(3)点M的坐标为M1(2,3),M2(2,1﹣2
);(3)点M的坐标为M1(2,3),M2(2,1﹣2![]() ),M3(2,1+2
),M3(2,1+2![]() )
)
【解析】
(1)用待定系数法法求解;把已知点的坐标分别代入解析式可得;
(2)设P(m,m2﹣4m+3),将点B(3,0)、C(0,3)代入得直线BC解析式为yBC=﹣x+3.过点P作y轴的平行线交直线BC于点D,则D(m,﹣m+3),PD==﹣(m﹣![]() )2+
)2+![]() ,求函数最值可得.
,求函数最值可得.
(3)设存在以点C、E、M、N为顶点的四边形是菱形.根据题意,点E(2,1),EF=CF=2,求出EC=2![]() ,根据菱形性质,ME=EC=2
,根据菱形性质,ME=EC=2![]() ,可求出M的坐标;注意当EM=EF=2时,M(2,3).
,可求出M的坐标;注意当EM=EF=2时,M(2,3).
解:(1)∵抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与
y轴交于点C,

∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)如图:
设P(m,m2﹣4m+3),
将点B(3,0)、C(0,3)代入得直线BC解析式为yBC=﹣x+3.
∵过点P作y轴的平行线交直线BC于点D,
∴D(m,﹣m+3),
∴PD=(﹣m+3)﹣(m2﹣4m+3)=﹣m2+3m.
=﹣(m﹣![]() )2+
)2+![]() .
.
∴当m=![]() 时,PD有最大值.
时,PD有最大值.
当m=![]() 时,m2﹣4m+3=﹣
时,m2﹣4m+3=﹣![]() .
.
∴P(![]() ,﹣
,﹣![]() ).
).
答:PD的长度最大时点P的坐标为(![]() ,﹣
,﹣![]() ).
).
(3)存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形.
根据题意,点E(2,1),
∴EF=CF=2,
∴EC=2![]() ,
,
根据菱形的四条边相等,
∴ME=EC=2![]() ,
,
∴M(2,1﹣2![]() )或(2,1+2
)或(2,1+2![]() )
)
当EM=EF=2时,M(2,3)
答:点M的坐标为M1(2,3),M2(2,1﹣2![]() ),M3(2,1+2
),M3(2,1+2![]() ).
).


科目:初中数学 来源: 题型:
【题目】为了解某学校兴趣小组活动情况,随机抽取了部分同学进行调查,按A:艺术,B:科技,C:体育,D:其他四个项目进行统计,绘制了两幅统计图(均不完整),请根据统计图解答以下问题:
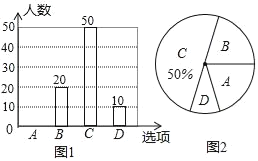
(1)本次接受问卷调查的共有 人:在扇形统计图中“D”选项所占的百分比为 ;
(2)扇形统计图中,“B”选项所对应扇形圆心角为 度;
(3)请补全条形统计图;
(4)若全校有2000人,请你估算一下全校喜欢艺术类学生的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线ABy=kx﹣1分别交x轴、y轴于点A、B,直线CDy=x+2分别交x轴、y轴于点D、C,且直线AB、CD交于点E,E的横坐标为﹣6.
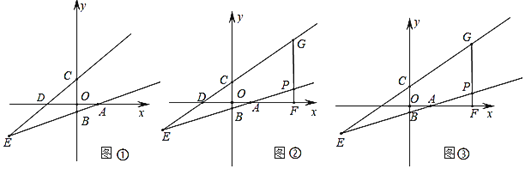
(1)如图①,求直线AB的解析式;
(2)如图②,点P为直线BA第一象限上一点,过P作y轴的平行线交直线CD于G,交x轴于F,在线段PG取点N,在线段AF上取点Q,使GN=QF,在DG上取点M,连接MN、QN,若∠GMN=∠QNF,求![]() 的值;
的值;
(3)在(2)的条件下,点E关于x轴对称点为T,连接MP、TQ,若MP∥TQ,且GN:NP=4:3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:


(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
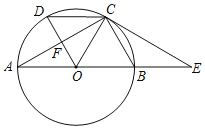
【题目】AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴下方的抛物线上一动点(包含点
轴下方的抛物线上一动点(包含点![]() ,
,![]() ).作直线
).作直线![]() ,若过点
,若过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)在点![]() 运动的过程中,请求出
运动的过程中,请求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使
,使![]() 是等腰三角形.若存在,请直接写出点
是等腰三角形.若存在,请直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·泰安)如图,是将抛物线![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.

(1)求抛物线的函数表达式;
(2)若点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 是抛物线上一点,点
是抛物线上一点,点![]() 是一次函数
是一次函数![]() 的图象上一点,若四边形
的图象上一点,若四边形![]() 为平行四边形,这样的点
为平行四边形,这样的点![]() 是否存在?若存在,分别求出点
是否存在?若存在,分别求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com