
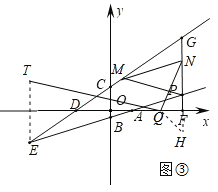
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��ABy��kx��1�ֱ�x�ᡢy���ڵ�A��B��ֱ��CDy��x+2�ֱ�x�ᡢy���ڵ�D��C����ֱ��AB��CD���ڵ�E��E�ĺ�����Ϊ��6��
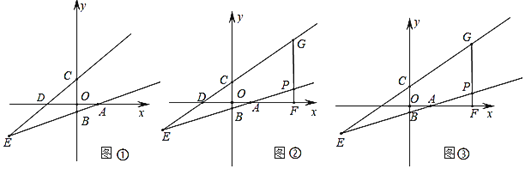
(1)��ͼ�٣���ֱ��AB�Ľ���ʽ��
(2)��ͼ�ڣ���PΪֱ��BA��һ������һ�㣬��P��y���ƽ���߽�ֱ��CD��G����x����F�����߶�PGȡ��N�����߶�AF��ȡ��Q��ʹGN��QF����DG��ȡ��M������MN��QN������GMN����QNF����![]() ��ֵ��
��ֵ��
(3)��(2)�������£���E����x��ԳƵ�ΪT������MP��TQ����MP��TQ����GN��NP��4��3�����P�����꣮
���𰸡�(1)y��![]() x��1��(2)
x��1��(2)![]() =
=![]() ��(3)��P����Ϊ(8��3).
��(3)��P����Ϊ(8��3).
��������
(1)�ѵ�E���������ֱ��CD��õ�E�����꣬�ٴ���ֱ��y��kx��1�У������ֱ��AB�Ľ���ʽ��
(2)�������C��D����õ�����Rt��OCD����GF��y��á�DGFҲ�ǵ���ֱ�������Σ���DG��![]() FG�����ӳ��ӳ�GF��H��ʹFH��FQ�������ֱ�������Σ�֤����GMN�ס�HNQ���ɶ�Ӧ�߶γɱ�����NH��
FG�����ӳ��ӳ�GF��H��ʹFH��FQ�������ֱ�������Σ�֤����GMN�ס�HNQ���ɶ�Ӧ�߶γɱ�����NH��![]() MG����ͨ��ת��֤��FG��NH���������õ�DG��2MG����MΪDG�е㣬�������
MG����ͨ��ת��֤��FG��NH���������õ�DG��2MG����MΪDG�е㣬�������![]() =
=![]() ��
��
(3)���P������Ϊp��������p��ʾG��F��M�����꣬������p��ʾGP�ij�����GN��NP��4��3�������p��ʾGN��ʽ�ӣ�����ΪGN��QF��������p��ʾQ�����꣮�����T���꣬�����ô���ϵ������ֱ��TQ����ʽ��һ����ϵ��a��ʽ��(��p)��ͬ������ֱ��MP����ʽ��һ����ϵ��c��ʽ��(��p)����MP��TQ�ɵ�a��c�����еù���p�ķ��̣����p���õ�P���꣮
�⣺(1)��x����6����y��x+2�е�y����4
��E(��6����4)��
��E(��6����4)����y��kx��1��
�é�4����6k��1�����k��![]() ��
��
��ֱ��AB�Ľ���ʽΪy��![]() x��1
x��1
(2)��ͼ�ڣ��ӳ�GF��H��ʹFH��FQ������QH��
�ߡ�QFH��90����GN��QF
��QH��![]() FQ��
FQ��![]() GN����NHQ��45��
GN����NHQ��45��
��y��x+2����x��0����y��2����y��0����x����2��
��C(0��2)��D(��2��0)��
��OC��OD��2
�ߡ�COD��90��
���OCD����ODC��45��
��FG��OC
���DGF����DCO��45������DFG����COD��90��
��DG��![]() FG����MGN����NHQ��45��
FG����MGN����NHQ��45��
�ߡ�GMN����QNF
���GMN�ס�HNQ
��![]()
��NH��![]() MG
MG
��GN��FQ��FH
��FN+GN��FN+FH����FG��NH
��DG��![]() FG��
FG��![]() NH��
NH��![]() ��
��![]() MG��2MG
MG��2MG
��DG��DM+MG��2MG
��DM��MG��![]() DG
DG
��![]() =
=![]() =
=![]()
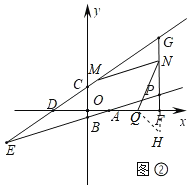
(3)��ͼ�ۣ���T��E����x��Գƣ�
��T(��6��4)
�ߵ�P��ֱ��BA��һ������
�����P����Ϊ(p��![]() p��1)(p��2)
p��1)(p��2)
��FG��y��
��F(p��0)��G(p��p+2)��
��PF��![]() p��1��GF��p+2
p��1��GF��p+2
��GP��GF��PF��![]() p+3
p+3
��GN��NP��4��3
��FQ��GN��![]() GP��
GP��![]()
��xQ��p��![]() ����Q(
����Q(![]() ��0)
��0)
��ֱ��TQ����ʽΪ��y��ax+b
��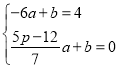 ��ã�a��
��ã�a��![]()
��![]() =
=![]() ������MΪDG�е�
������MΪDG�е�
��M(![]() ��
��![]() )
)
��ֱ��MP����ʽΪ��y��cx+d
��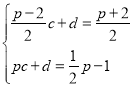 ��ã�c��
��ã�c��![]()
��MP��TQ
��a��c����![]()
��ã�p��8
���P����Ϊ(8��3)


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̽����
��1����ͼ1���ȱߡ�ABC����һ��P����AP��8��BP��15��CP��17�����APB�Ĵ�С������ʾ������ABP�ƶ���A��ת����ACP������
��2����ͼ2���ڡ�ABC�У���CAB��90����AB��AC��E��FΪBC�ϵĵ㣬�ҡ�EAF��45������֤��EF2��BE2+FC2��
��3����ͼ3���ڡ�ABC�У���C��90������ABC��30������OΪ��ABC��һ�㣬����AO��BO��CO���ҡ�AOC����COB����BOA��120������AC��1����OA+OB+OC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
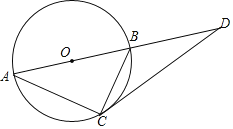
����Ŀ����ͼ����֪AB����O��ֱ����DC����O�����ڵ�C����AB���ӳ����ڵ�D��
��1����֤����BAC����BCD��
��2����BD��4��DC��6������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������н�������֪��ijУѧ����������Ȼ���������˽�̶ȣ��ڸ�У�����ȡ�˲���ѧ�������ʾ����ʾ��������ĸ�ѡ�A��ʮ���˽⣻B���˽�϶ࣺC���˽���٣�D�����˽⣨Ҫ��ÿ���������ѧ����ѡ��ֻ��ѡ��һ����ֽ�����Ľ�����Ƴ�������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
��1�����α���ȡ��ѧ������_______����
��2���벹ȫ����ͼ��
��3������ͼ�е�ѡ�C���˽���١�������ռ���ε�Բ�ĽǵĴ�СΪ_______�㣻
��4������У����![]() ��ѧ������������������������Ƹ�У����������Ȼ��������ʮ���˽⡱�͡��˽�϶ࡱ��ѧ�����ж�������
��ѧ������������������������Ƹ�У����������Ȼ��������ʮ���˽⡱�͡��˽�϶ࡱ��ѧ�����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijר������A��B������Ʒ����֪�ڴ���ǰ����60��A��Ʒ��30��B��Ʒ����1080Ԫ����50��A��Ʒ��10��B��Ʒ����840Ԫ��A��B������Ʒ����ͬ���Ժ�ij����500��A��Ʒ��450��B��Ʒһ���Ȳ������ٻ�1960Ԫ������A��B������Ʒ����ǰ������Ǯ�����˶����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУֲ����·���������β�����Ƴ����ɸ�ȫ������ͼ����ÿ����һ������ͼ�������γ��Ⱦ�����dcm����ͼ��ʾ����֪ÿ������ͼ���ı߳�Ϊ10![]() cm������һ���ڽ�Ϊ60�㣮
cm������һ���ڽ�Ϊ60�㣮
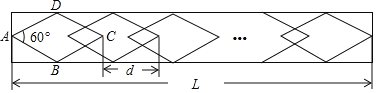
(1)��һ������ͼ��ˮƽ����ĶԽ��߳���
(2)��d��26�����εij���L�ܷ���6010cm�����ܣ�������θ����������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C��Բ����һ�㣬����AC��BC���Ե�CΪ�˵�������CD��CP�ֱ��߶�AB����ֱ���ڵ�D��P��ʹ��1����2����A��

��1����֤��ֱ��PC����O�����ߣ�
��2����CD��4��BD��2�����߶�BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
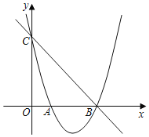
����Ŀ����ͼ����֪������y=ax2+bx+3(a��0)������A(1��0)�͵�B(3��0)����y�ύ�ڵ�C��
(1)��������ߵĽ���ʽ��
(2)����P��ֱ��BC�·�����������һ����(����B��C�غ�)������P��y���ƽ���߽�ֱ��BC�ڵ�D����PD�ij������ʱ��P�����꣮
(3)�������ߵĶԳ�����BC���ڵ�E����M�������ߵĶԳ�����һ�㣬NΪy����һ�㣬�Ƿ���������ĵ�M�͵�N��ʹ���Ե�C��E��M��NΪ������ı��������Σ�������ڣ���ֱ��д����M�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���������˵�����ģ�⿼�ԣ���У�쵼Ϊ���˽�ѧ������ѧ����������������鲿��ѧ������ѧ�ɼ����������������ݽ���������������
�����·���������������
�ȼ��ȼ� | ������ | �����ܷ� | ���� |
A | 110��X��120 | P | 4 |
B | 100��X��110 | 843 | n |
C | 90��X��100 | 574 | m |
D | 80��X��90 | 171 | 2 |
�����������������ͳ��ͼ��

��1�����m���� ����n���� ������ѧ�ɼ�����λ�����ڵĵȼ��� ����
��2�������У��1200��ѧ���μ��˱���ģ��⣬����D�ȼ���������
��3����֪��������ѧ������ѧ�ɼ�ƽ����Ϊ102�֣���A�ȼ�ѧ������ѧ�ɼ���ƽ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com