
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】D
【解析】分析:A、把m=-3代入[2m,1-m,-1-m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
B、令函数值为0,求得与x轴交点坐标,利用两点间距离公式解决问题;
C、首先求得对称轴,利用二次函数的性质解答即可;
D、根据特征数的特点,直接得出x的值,进一步验证即可解答.
详解:
因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m];
A、当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣![]() )2+
)2+![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() );此结论正确;
);此结论正确;
B、当m>0时,令y=0,有2mx2+(1﹣m)x+(﹣1﹣m)=0,解得:x1=1,x2=﹣![]() ﹣
﹣![]() ,
,
|x2﹣x1|=![]() +
+![]() >
>![]() ,所以当m>0时,函数图象截x轴所得的线段长度大于
,所以当m>0时,函数图象截x轴所得的线段长度大于![]() ,此结论正确;
,此结论正确;
C、当x=1时,y=2mx2+(1﹣m)x+(﹣1﹣m)=2m+(1﹣m)+(﹣1﹣m)=0 即对任意m,函数图象都经过点(1,0)那么同样的:当m=0时,函数图象都经过同一个点(1,0),当m≠0时,函数图象经过同一个点(1,0),故当m≠0时,函数图象经过x轴上一个定点此结论正确.
D、当m<0时,y=2mx2+(1﹣m)x+(﹣1﹣m) 是一个开口向下的抛物线,其对称轴是:直线x=![]() ,在对称轴的右边y随x的增大而减小.因为当m<0时,
,在对称轴的右边y随x的增大而减小.因为当m<0时,![]() ,即对称轴在x=
,即对称轴在x=![]() 右边,因此函数在x=
右边,因此函数在x=![]() 右边先递增到对称轴位置,再递减,此结论错误;
右边先递增到对称轴位置,再递减,此结论错误;
根据上面的分析,①②③都是正确的,④是错误的.
故选:D.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
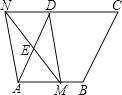
【题目】如图,在菱形ABCD中,AB=5,∠DAB=60°,点E是AD边的中点.点M是线段AB上的一个动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
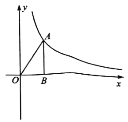
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]()
![]() 的图象上一点过点
的图象上一点过点![]() 作
作![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 和
和![]() 的值.
的值.
(2)直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与反比例函数图象交于点
,与反比例函数图象交于点![]() .
.
①若![]() ,求点
,求点![]() 坐标;②若点
坐标;②若点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
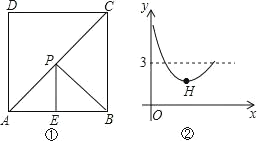
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点。设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为( )
A. (1,2)B. (![]() )C.
)C. 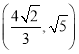 D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-7平移后的图象l经过点(-3,-2),
(1)求l的函数解析式;并画出该函数的图象;
(2)l与x轴交于点A,点P是l上一点,且S△AOP=![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
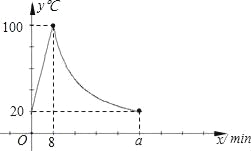
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年奉节脐橙喜获丰收,某村委会将全村农户的脐橙统一装箱出售.经核算,每箱成本为40元,统一零售价定为每箱50元,可以根据买家订货量的多少给出不同的折扣价销售.
(1)问最多打几折销售,才能保证每箱脐橙的利润率不低于10%?
(2)该村最开始几天每天可卖5000箱,因脐橙的保鲜周期短,需要尽快打开销路,减少积压,村委会决定在零售价基础上每箱降价3m%,这样每天可多销售![]() m%;为了保护农户的收益与种植积极性,政府用“精准扶贫基金”给该村按每箱脐橙m元给予补贴进行奖励,结果该村每天脐橙销售的利润为49000元,求m的值.
m%;为了保护农户的收益与种植积极性,政府用“精准扶贫基金”给该村按每箱脐橙m元给予补贴进行奖励,结果该村每天脐橙销售的利润为49000元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com