
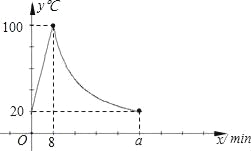
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |
【答案】(1)当0≤x≤8时,y=10x+20; 当8<x≤a时,![]() ;(2)a=40;(3)在7:20或7:38~7:45时打开饮水机.
;(2)a=40;(3)在7:20或7:38~7:45时打开饮水机.
【解析】分析:(1)由函数图象可设函数解析式,再由图中坐标代入解析式,即可求得y与x的关系式;
(2)将y=20代入y=![]() ,即可得到a的值;
,即可得到a的值;
(3)要想喝到不超过40℃的热水,让解析式小于等于40,则可得x的取值范围,再由题意可知开饮水机的时间.
详解:
(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)代入y=k1x+b
得k1=10,b=20
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,设y=![]() ,
,
将(8,100)代入y=![]()
得k2=800
∴当8<x≤a时,y=![]() ;
;
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,y=![]() ;
;
(2)将y=20代入y=![]() ,
,
解得a=40;
(3)要想喝到不超过40℃的热水,则:
∵10x+20≤40,
∴0<x≤2,
∵![]() ≤40,
≤40,
∴20≤x<40
因为40分钟为一个循环,
所以8:20喝到不超过40℃的开水,
则需要在8:20﹣(40+20)分钟=7:20
或在(8:20﹣40分钟)﹣2分钟=7:38~7:45打开饮水机
故在7:20或7:38~7:45时打开饮水机.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
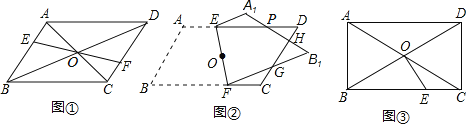
【题目】已知:平行四边形ABCD的对角线AC,BD相交于点O.
(1)如图①,EF过点O且与AB,CD分别相交于点E、F,AC=6,△AEO的周长为10,求CF+OF的值.
(2)如图②,将平行四边形ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD、DE于点H、P,请在折叠后的图形中找一条线段,使它与EP相等,并加以证明.
(3)如图③,△ABO是等边三角形,AB=1,点E在BC边上,且BE=1,则2EC-2EO= 直接填结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
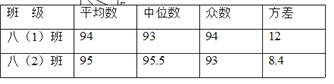
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 与
与![]() 的图象如图所示,则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正确的个数是()
的图象如图所示,则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正确的个数是()

A. 3个B. 2个C. 1个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com