
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】(1)A、B两种净水器的销售单价分别为2500元、2100元;(2)超市最多采购A种型号净水器10台时,采购金额不多于54000元;(3)采购A种型号净水器8台,采购B种型号净水器22台,公司能实现利润12800元的目标.
【解析】设A、B两种净水器的销售单价分别为x元,y元,
由题意得:![]()
答:A、B两种净水器的销售单价分别为2500元,2100元.
设采购A种型号的净水器a台,则B种净水器(30—a)台.
由题意得:2000a+1700(30-a)![]()
解得:![]()
故超市最多采购A种型号净水器10台,采购金额不多于54000元.
由题意得:![]()
解得a=8,
故采购A种型号净水器8台,B种型号净水器22台,公司能实现12800元的目标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点。设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为( )
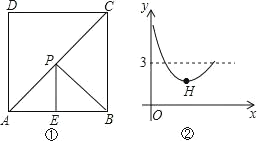
A. (1,2)B. (![]() )C.
)C. 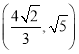 D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
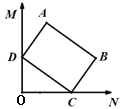
【题目】如图,∠MON=90°,矩形ABCD的顶点C、D分别在边ON,OM上滑动,AB=9,BC=6,在滑动过程中,点A到点O的最大距离为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
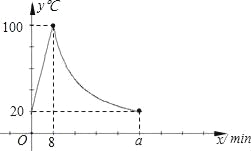
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 的度数是
的度数是![]() 的度数的k倍,则规定
的度数的k倍,则规定![]() 是
是![]() 的k倍角.
的k倍角.
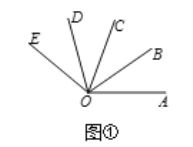
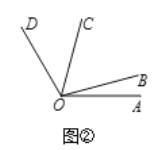
(1)若∠M=21°17',则∠M的5倍角的度数为 ;
(2)如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;
(3)如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠ABC,∠ACB的平分线相交于F点,过点F作DE∥BC,交AB于点D,交AC于点E.
(1)请你写出图中所有的等腰三角形;
(2)请写出BD,CE,DE之间的数量关系;
(3)并对第(2)问中BD,CE,DE之间的数量关系给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
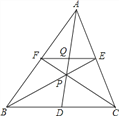
【题目】已知,如图,P为△ABC中线AD上一点,AP:PD=2:1,延长BP、CP分别交AC、AB于点E、F,EF交AD于点Q.(1)PQ=EQ;(2)FP:PC=EC:AE;(3)FQ:BD=PQ:PD;(4)S△FPQ:S△DCP=SPEF:S△PBC.上述结论中,正确的有_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com