
【题目】若![]() 的度数是
的度数是![]() 的度数的k倍,则规定
的度数的k倍,则规定![]() 是
是![]() 的k倍角.
的k倍角.
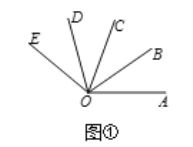
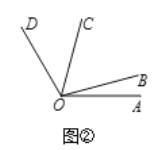
(1)若∠M=21°17',则∠M的5倍角的度数为 ;
(2)如图1,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=∠COE,请直接写出图中∠AOB的所有3倍角;
(3)如图2,若∠AOC是∠AOB的5倍角,∠COD是∠AOB的3倍角,且∠AOC和∠BOD互为补角,求∠AOD的度数.
【答案】(1)106°25';(2)∠AOD,∠BOE;(3)120°.
【解析】
(1)根据题意,列式计算即可得到答案;
(2)由角平分线性质定理,结合∠AOC=∠COE,得到∠AOB=∠BOC=∠COD=∠DOE,即可得到∠AOD=3∠AOB,∠BOE=3∠AOB;
(3)设∠AOB=x,则∠AOC=5x,∠BOC=4x,∠COD=3x,则利用∠AOC和∠BOD互为补角的关系,列出方程,即可得到x的值,然后得到答案.
解:(1)![]() ;
;
故答案为:![]() .
.
(2)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOC=∠COE,
∴∠AOB=∠BOC=∠COD=∠DOE,
∴∠AOD=3∠AOB,∠BOE=3∠AOB;
∴图中∠AOB的所有3倍角有:∠AOD,∠BOE;
(3)设∠AOB=x,则∠AOC=5x,∠COD=3x.
∴∠BOC=4x,
∵∠AOC和∠BOD互为补角,
∴∠AOC+∠BOD=∠AOC+∠BOC+∠COD=180°,
即5x+7x=180°,
解得:x=15°.
∴∠AOD=8x=120°.


科目:初中数学 来源: 题型:
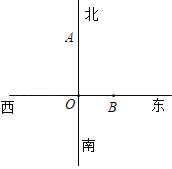
【题目】如图,一艘货轮位于O地,发现灯塔A在它的正北方向上,这艘货轮沿正东方向航行50千米,到达B地,此时用雷达测得灯塔A与货轮的距离为100千米.
(1)在图中作出灯塔A的位置,并作射线BA;
(2)以正北,正南方向为基准,借助量角器,描述灯塔A在B地的什么方向上(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
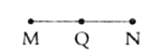
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
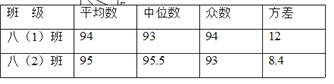
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
查看答案和解析>>
科目:初中数学 来源: 题型:
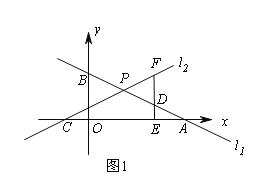
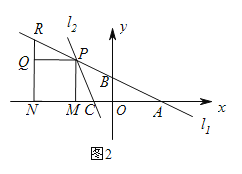
【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
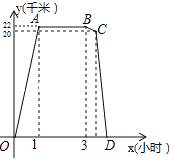
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
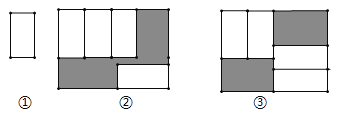
【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为
)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为![]() ,图③中阴影部分的周长为
,图③中阴影部分的周长为![]() ,则
,则![]() ___________.
___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com