
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.

【答案】(1)⊙M的半径为5,M(4,3);(2)点C在⊙M上,理由见解析;(3)y2=![]() ,,y2>y1>0时,0<x<2
,,y2>y1>0时,0<x<2![]()
【解析】试题分析:(1)先确定出AB=10,进而求出圆M的半径,最后用线段的中点坐标公式即可得出结论;
(2)求出CM=5和圆M的半径比较大小,即可得出结论;
(3)先确定出直线和双曲线解析式,即可求出两图象的交点坐标,即可得出结论.
试题解析:
(1)∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(8,0),B(0,6),
∴AB=![]() =10,
=10,
∴⊙M的半径为5,
由线段中点坐标公式x=,y=![]() ,得x=4,y=3,
,得x=4,y=3,
∴M(4,3),
(2)点C在⊙M上,
理由:∵C(1,7),M(4,3),
∴CM=![]() =5,
=5,
∴点C在⊙M上;
(3)由题意知,y1=x,
设反比例函数的解析式为y2=![]() (k≠0),
(k≠0),
∵M(4,3)在反比例函数图象上,
∴k=3×4=12,
∴反比例函数的解析式为y2=![]() ,
,
当y1=y2时,x=![]() ,
,
∴x=±2![]() ,
,
∴由图象知,当y2>y1>0时,0<x<2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
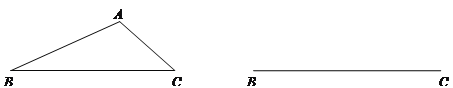
查看答案和解析>>
科目:初中数学 来源: 题型:
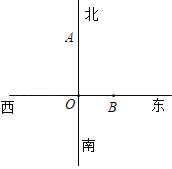
【题目】如图,一艘货轮位于O地,发现灯塔A在它的正北方向上,这艘货轮沿正东方向航行50千米,到达B地,此时用雷达测得灯塔A与货轮的距离为100千米.
(1)在图中作出灯塔A的位置,并作射线BA;
(2)以正北,正南方向为基准,借助量角器,描述灯塔A在B地的什么方向上(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
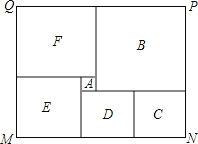
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
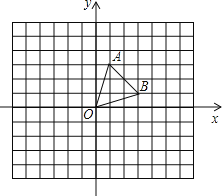
【题目】如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),
(1)请画出把△ABO向下平移5个单位后得到的△A1B1O1的图形;
(2)请画出将△ABO绕点O顺时针旋转90°后得到的△A2B2O2,并写出点A的对应点A2的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
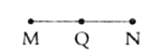
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
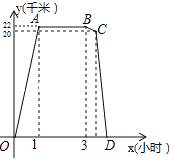
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com