
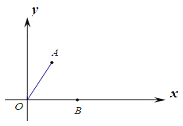
【题目】如图,在平面直角坐标系中,A(1,![]() ),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________.
),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________.
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,数![]() 所对应的点与原点的距离叫做数
所对应的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]()
提出问题:(1)点![]() 所表示的数如图所示,则
所表示的数如图所示,则![]() 两点间的距离是 ,
两点间的距离是 ,![]() 两点间的距离是_____,
两点间的距离是_____,![]() 两点间的距离是 .
两点间的距离是 .
探究结论:(2)在数轴上,若![]() 两点对应的数分别是
两点对应的数分别是![]() ,则
,则![]() ____ (用含有
____ (用含有![]() 的式子表示).
的式子表示).
拓展应用:(3)请利用.上述结论,解决下列问题:
①![]() 和
和![]() 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为
②![]()
③满足![]() 的未知数的值为
的未知数的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
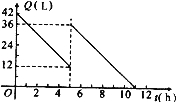
(1)机动车行驶 h后加油;
(2)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
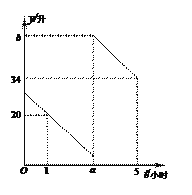
【题目】张师傅驾驶某种型号轿车从甲地去乙地,该种型号轿车每百公里油耗为10升(每行驶100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根据仪表盘显示,油箱中还剩4升汽油.假设加油前轿车以80公里/小时的速度匀速行驶,加油后轿车以90公里/小时的速度匀速行驶(不计加油时间),已知油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系如图所示.
(1) 加油前,该轿车每小时消耗汔油 升;加油后,该轿车每小时消耗汔油 升;
(2)求加油前油箱剩余油量y(升)与行驶时间t(小时)之间的函数表达式;
(3)求张师傅在加油站加了多少升汽油.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x与直线y垂直于点O,点B,C在直线x上,点A在直线x外,连接AC,AB得到△ABC.
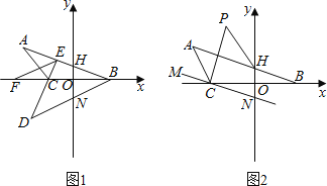
(1)将△ABC沿直线x折叠,使点A落在点D处,延长DC交AB于点E,EF平分∠AED交直线x于点F.
①若∠EFB=25°,∠DEF=10°,则∠DCF=______
②若∠ACF-∠AEF=18°,求∠EFB的度数;
(2)过点C作MN平行于AB交直线y于点N,CP平分∠BCM,HP平分∠AHY,当点C从点O沿直线x向左运动时,∠CPH的度数是否发生变化?若不变求其度数;若变化,求其变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com