
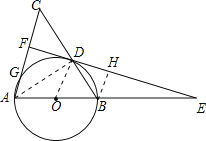
【题目】(白云区校级二模)如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.

(1)连接OD,则OD与AC的位置关系是 .
(2)求AC的长.
(3)求sinE的值.
【答案】(1)平行;(2)10;(3)![]()
【解析】
(1)连接OD,由EF为圆O的切线,利用切线的性质得到OD⊥EF,再由AF⊥EF,可得OD∥AC;
(2)根据O为AB的中点,且OD与AF平行,得到OD为三角形ABC的中位线,得到OD为AC的一半,由OD的长求出AC的长即可;
(3)由(2)得到D为BC中点,求出BD与DC长,过B点作EF的垂线BH,垂足为H点,连接AD,可得BH,OD,AC三直线平行,由AB为圆O的直径,利用直径所对的圆周角为直角,得到∠ADB=90°,再利用弦切角等于夹弧所对的圆周角,得到三角形DBH与三角形ABD相似,由相似得比例求出BH的长,再由BH与OD平行得到三角形BHE与三角形ODE相似,由相似得比例求出BE的长,在直角三角形BHE中,利用锐角三角函数定义求出sinE的值即可.
(1)连接OD,则OD与AC的位置关系是平行,
理由:∵EF与圆O相切,
∴OD⊥EF,
∵AF⊥EF,
∴OD∥AC;
故答案为:平行;
(2)∵O为AB中点,OD∥AC,且OD=AO=OB=5,
∴OD为△BAC的中位线,
∴OD![]() AC,
AC,
∴AC=2OD=10;
(3)由(2)知D为BC的中点,
∴BD=CD=6,
过B点作EF的垂线BH,垂足为H点,连接AD,
则有BH∥OD∥AC,
∵AB是直径,
∴∠ADB=90°,
∵∠HDB=∠DAB,∠ADB=∠DHB=90°,
∴△DBH∽△ABD,
∴![]() ,即
,即![]() ,
,
解得:BH=![]() ,
,
设BE=x,
∵BH∥OD,
∴△EHB∽△EDO,
∴![]() ,即
,即![]() ,
,
解得:x![]() ,即BE
,即BE![]() ,
,
∴sinE![]()
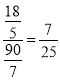 .
.


科目:初中数学 来源: 题型:
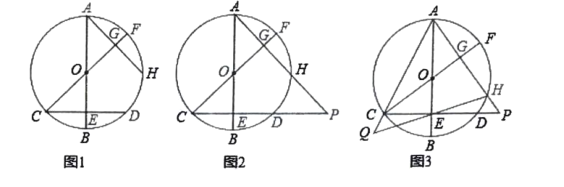
【题目】已知:![]() 都是
都是![]() 的直径,
的直径,![]() 都是
都是![]() 的弦,
的弦,![]() 于点
于点![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,延长![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,延长![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
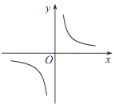
【题目】已知反比例函数 y=![]() 的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A.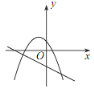 B.
B.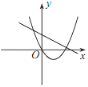 C.
C.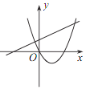 D.
D.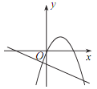
查看答案和解析>>
科目:初中数学 来源: 题型:
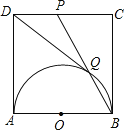
【题目】如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是______
,其中正确结论是______![]() 填写序号
填写序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
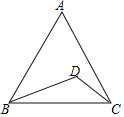
【题目】如图,在等边△ABC内任取一点D,连接CD,BD得到△CDB,如果等边△ABC内每一点被取到的可能性都相同,则△CBD是钝角三角形的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan67°≈
,tan67°≈![]() ,sin67°≈
,sin67°≈![]() ,cos67°≈
,cos67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
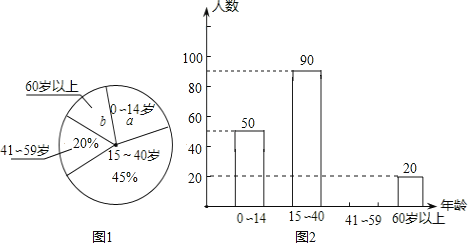
【题目】小丽同学学习了统计知识后,带领班级“课外活动小组”,随机调查了某辖区若干名居民的年龄,并将调查数据绘制成图①和图②两幅尚不完整的统计图.
请你根据图中的信息,解答下列各题:
(1)共抽查了_____名居民的年龄,扇形统计图中![]() _____,
_____,![]() ______;
______;
(2)补全条形统计图;
(3)若该辖区居民约有2600人,请你估计年龄在15~59岁的居民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
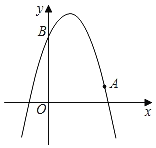
(1)求该二次函数的表达式及顶点坐标;
(2)点C(m,n)在该二次函数图象上.
①当m=﹣1时,求n的值;
②当m≤x≤3时,n最大值为5,最小值为1,请根据图象直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com