
【题目】如图,已知二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
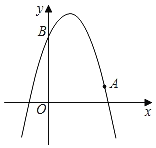
(1)求该二次函数的表达式及顶点坐标;
(2)点C(m,n)在该二次函数图象上.
①当m=﹣1时,求n的值;
②当m≤x≤3时,n最大值为5,最小值为1,请根据图象直接写出m的取值范围.
【答案】(1)y=﹣(x﹣1)2+5,顶点为(1,5);(2)①n=1;②﹣1≤m≤1
【解析】
(1)根据待定系数法即可求得;
(2)①把x=﹣1代入(1)中求得的解析式求得函数y的值,即可求得n的值;
②把y=1代入抛物线解析式求得对应的x的值,然后根据图象即可求得m的取值范围.
解:(1)∵二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
∴![]() ,解得
,解得![]() ,
,
∴该二次函数为y=﹣x2+2x+4,
∵y=﹣(x﹣1)2+5,
∴顶点为(1,5);
(2)∵点C(m,n)在该二次函数图象上,
①当m=﹣1时,则C(﹣1,n),
把C(﹣1,n)代入y=﹣x2+2x+4得,
n=-1-2+4=1,
∴n=1;
②∵y=﹣(x﹣1)2+5,
∴当x=3时,y=﹣(3﹣1)2+5=1,抛物线对称轴是直线x=1,函数的最大值是5,
∴点(3,1)关于关于对称轴的对称点是(-1,1),抛物线的顶点为(1,5).
∵当m≤x≤3时,n最大值为5,最小值为1,
∴m的取值范围是-1≤m≤1.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(白云区校级二模)如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.

(1)连接OD,则OD与AC的位置关系是 .
(2)求AC的长.
(3)求sinE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
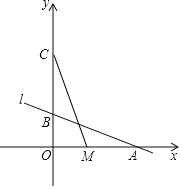
【题目】如图,直线l:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;
(3)设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
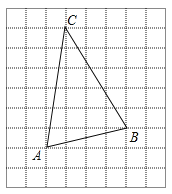
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均落在格点上,
均落在格点上,
(1)![]() 的长等于________;
的长等于________;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
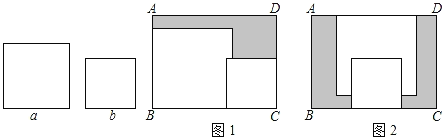
A.aB.bC.ADD.AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )
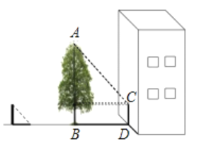
A.6.0mB.5.0mC.4.0mD.3.0m
查看答案和解析>>
科目:初中数学 来源: 题型:
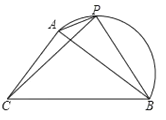
【题目】如图,在△ABC中,AB=4cm.BC=5cm,P是![]() 上的动点.设A,P两点间的距离为xcm,
上的动点.设A,P两点间的距离为xcm,
B,P两点间的距离为![]() cm,C,P两点间的距离为
cm,C,P两点间的距离为![]() cm.
cm.
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 |
| 4.00 | 3.69 | 2.13 | 0 | |
| 3.00 | 3.91 | 4.71 | 5.23 | 5 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象:
的图象:
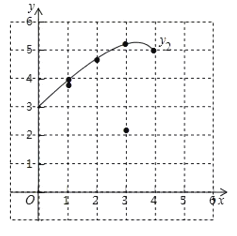
(3)结合函数图象.
①当△PBC为等腰三角形时,AP的长度约为____cm.
②记![]() 所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.
所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形![]() 是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结
是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,则
,则![]() 的长为( )
的长为( )
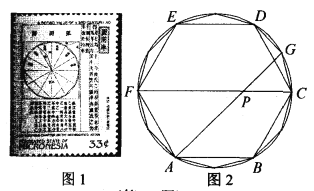
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,与抛物线
的图象与y轴交于点A,与抛物线![]() 的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
(1)求出抛物线的对称轴和点C坐标;
(2)①当![]() 时,直接写出抛物线
时,直接写出抛物线![]() 与图形G的公共点个数.
与图形G的公共点个数.
②如果抛物线![]() 与图形G有且只有一个公共点,求出a的取值范围.
与图形G有且只有一个公共点,求出a的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com