练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

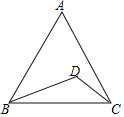
    【题目】如图，在等边△ABC内任取一点D，连接CD，BD得到△CDB，如果等边△ABC内每一点被取到的可能性都相同，则△CBD是钝角三角形的概率是______．

    【答案】

    【解析】

    由题意通过圆和三角形的知识画出满足条件的图形，分别找出满足条件的点集对应的图形面积及图形的总面积，再根据概率公式即可得出答案．

    解：如图，取BC的中点O，以O为圆心，BC为直径画半圆，交AB于E，连接OE，

    当D在半圆上时，∠BDC＝90°，

    ∵△CBD是钝角三角形时，只能∠BDC＞90°，

    ∴点D落在如图所示的半圆O内时，△CBD是钝角三角形，

    设等边三角形的边长为2a，

    半圆的面积为，

    等边△ABC的面积是＝a2，

    ∴满足∠BDC＞90°的概率是＝，

    ∴△CBD是钝角三角形的概率；

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】实验室里，水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器（甲、丙的底面积相同），用两个相同的管子在容器的6cm高度处连通（即管子底离容器底6，管子的体积忽略不计），、现在三个容器中，只有甲中有水，水位高2，如图①所示，若每分钟同时向乙、丙中注入相同量的水，到三个容器都注满水停止，乙、丙容器中的水位（）与注水时间（）的图象如图②所示．

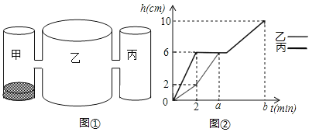
    （1）乙、丙两个容器的底面积之比为 ．

    （2）图②中的值为 ，的值为 ．

    （3）注水多少分钟后，乙与甲的水位相差2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形是平行四边形，连接对角线，过点作与的延长线交于点，连接交于．

    （1）求证：；

    （2）连结，若，且，求证：四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

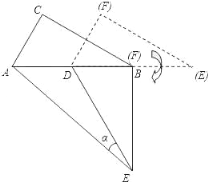
    【题目】两个全等的直角三角形 ABC 和 DEF 重叠在一起，其中∠A=60°，AC=1．固定△ABC 不动，将△DEF 进行如下操作：

    （1）如图，△DEF 沿线段 AB 向右平移（即 D 点在线段 AB 内移动），连接 DC、CF、FB，四边形 CDBF 的形状在不断的变化，但它的面积不变化，请求出其面积．

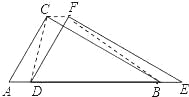
    （2）如图，当 D 点移到 AB 的中点时，请你猜想四边形CDBF 的形状，并说明理由．

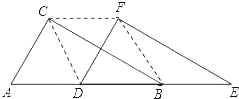
    （3）如图，△DEF 的 D 点固定在 AB 的中点，然后绕 D 点按顺时针方向旋转△DEF，使 DF 落在 AB 边上，此时 F 点恰好与 B 点重合，连接 AE，请你求出 sinα的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（白云区校级二模）如图，在△ABC中，AB＝10，BC＝12，以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F，交AB的延长线于点E.

    （1）连接OD，则OD与AC的位置关系是　 　.

    （2）求AC的长.

    （3）求sinE的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

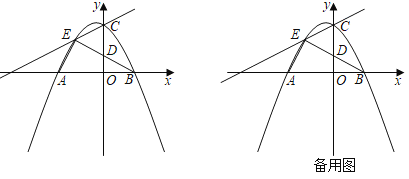
    【题目】如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c的图象与x轴交于A（﹣3，0）、B（2，0）两点，与y轴交于点C（0，3）．

    （1）求抛物线的解析式；

    （2）点E（m，2）是直线AC上方的抛物线上一点，连接EA、EB、EC，EB与y轴交于D．

    ①点F是x轴上一动点，连接EF，当以A、E、F为顶点的三角形与△BOD相似时，求出线段EF的长；

    ②点G为y轴左侧抛物线上一点，过点G作直线CE的垂线，垂足为H，若∠GCH＝∠EBA，请直接写出点H的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

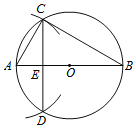
    【题目】已知⊙O．如图，

    （1）作⊙O的直径AB；

    （2）以点A为圆心，AO长为半径画弧，交⊙O于C，D两点；

    （3）连接CD交AB于点E，连接AC，BC．

    根据以上作图过程及所作图形，有下面三个推断：

    ①CE＝DE； ②BE＝3AE； ③BC＝2CE．

    所有正确推断的序号是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA＝2，OB＝1，斜边AC∥x轴．若反比例函数y（k＞0，x＞0）的图象经过AC的中点D，则k的值为（ ）

    A.4B.5C.6D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数学实践活动课上，小明同学打算通过测量树的影长计算树的高度，阳光下他测得长1m的竹竿落在地面上的影长为0.9m，在同一时刻测量树的影长时，他发现树的影子有一部分落在地面上，还有一部分落在墙面上，他测得这棵树落在地面上的影长BD为2.7m，落在墙面上的影长CD为1.0m，则这棵树的高度是（ ）

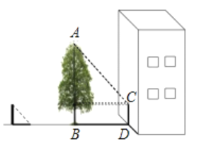
    A.6.0mB.5.0mC.4.0mD.3.0m

    查看答案和解析>>

    同步练习册答案