
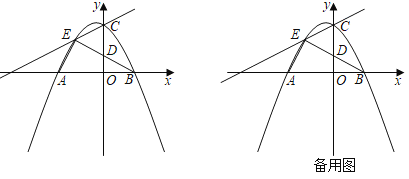
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩxOyÖÐĢŽÅŨÎïÏßyĢ―ax2+bx+cĩÄÍžÏóÓëxÖá―ŧÓÚAĢĻĐ3ĢŽ0ĢĐĄĒBĢĻ2ĢŽ0ĢĐÁ―ĩãĢŽÓëyÖá―ŧÓÚĩãCĢĻ0ĢŽ3ĢĐĢŪ
ĢĻ1ĢĐĮóÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐĩãEĢĻmĢŽ2ĢĐĘĮÖąÏßACÉÏ·―ĩÄÅŨÎïÏßÉÏŌŧĩãĢŽÁŽ―ÓEAĄĒEBĄĒECĢŽEBÓëyÖá―ŧÓÚDĢŪ
ĒŲĩãFĘĮxÖáÉÏŌŧķŊĩãĢŽÁŽ―ÓEFĢŽĩąŌÔAĄĒEĄĒFΊķĨĩãĩÄČý―ĮÐÎÓëĄũBODÏāËÆĘąĢŽĮóģöÏßķÎEFĩÄģĪĢŧ
ĒÚĩãGΊyÖáŨóēāÅŨÎïÏßÉÏŌŧĩãĢŽđýĩãGŨũÖąÏßCEĩÄīđÏßĢŽīđŨãΊHĢŽČôĄÏGCHĢ―ĄÏEBAĢŽĮëÖą―ÓÐīģöĩãHĩÄŨøąęĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐyĢ―Đ![]() x+3ĢŧĢĻ2ĢĐĒŲEFĩÄģĪΊ2
x+3ĢŧĢĻ2ĢĐĒŲEFĩÄģĪΊ2![]() ŧō2ĢŧĒÚĩãHĩÄŨøąęΊĢĻĐ
ŧō2ĢŧĒÚĩãHĩÄŨøąęΊĢĻĐ![]() ĢŽ
ĢŽ![]() ĢĐŧōĢĻĐ
ĢĐŧōĢĻĐ![]() ĢĐĢŪ
ĢĐĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐÓÃīýķĻÏĩĘý·ĻĮóģöšŊĘý―âÎöĘ―žīŋÉĢŧ
ĢĻ2ĢĐĒŲĩÃģö![]() ĢŽĩąĘąĢŽĩąĘąĢŽŋÉĮóģöĩÄģĪĢŧ
ĢŽĩąĘąĢŽĩąĘąĢŽŋÉĮóģöĩÄģĪĢŧ
ĒÚĢĻĒņĢĐĮóģöÖąÏß![]() ĩÄ―âÎöĘ―ÎŠ
ĩÄ―âÎöĘ―ÎŠ![]() ĢŽĩÃģö
ĢŽĩÃģö![]() ĢŽÔō
ĢŽÔō![]() ĢŽĩÃģö
ĢŽĩÃģö![]() ĢŽÓÉ
ĢŽÓÉ![]() ĢŽÉč
ĢŽÉč![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() ĢŽ―âĩÃĢŽ
ĢŽ―âĩÃĢŽ![]() ĢŽŋÉĮóģö
ĢŽŋÉĮóģö![]() ĩãĩÄŨøąęĢŧ
ĩãĩÄŨøąęĢŧ
ĢĻĒōĢĐđýĩã![]() Ũũ
Ũũ![]() ĢŽđýĩã
ĢŽđýĩã![]() Ũũ
Ũũ![]() ÓÚĩã
ÓÚĩã![]() ĢŽđýĩã
ĢŽđýĩã![]() Ũũ
Ũũ![]() ÓÚĩã
ÓÚĩã![]() ĢŽÖĪĩÃ
ĢŽÖĪĩÃ![]() ĢŽÓÉĢĻĒņĢĐÖŠĢš
ĢŽÓÉĢĻĒņĢĐÖŠĢš![]() ĢŽÔō
ĢŽÔō![]() ĢŽÉč
ĢŽÉč![]() ĢŽÔō
ĢŽÔō![]() ĢŽÖĪÃũ
ĢŽÖĪÃũ![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ![]() ĢŽÓÖ
ĢŽÓÖ![]() ĢŽĩÃģö
ĢŽĩÃģö![]() ĢŽīúČë
ĢŽīúČë![]() ÖÐĢŽĩÃ
ÖÐĢŽĩÃ![]() ĢŽŋÉĮóģö
ĢŽŋÉĮóģö![]() ĩãŨøąęĢŪ
ĩãŨøąęĢŪ
―âĢšĢĻ1ĢĐ―ŦAĢĻĐ3ĢŽ0ĢĐĄĒBĢĻ2ĢŽ0ĢĐĄĒCĢĻ0ĢŽ3ĢĐīúČëyĢ―ax2+bx+cĩÃĢŽ
 ĢŽ
ĢŽ
―âĩÃĢš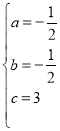 ĢŽ
ĢŽ
ĄāÅŨÎïÏßĩÄ―âÎöĘ―ÎŠĢšyĢ―Đ![]() x+3Ģŧ
x+3Ģŧ
ĢĻ2ĢĐĒŲ―ŦEĢĻmĢŽ2ĢĐīúČëyĢ―Đ![]() x+3ÖÐĢŽ
x+3ÖÐĢŽ
ĩÃĐ![]() m+3Ģ―0ĢŽ―âĩÃmĢ―Đ2ŧō1ĢĻÉáČĨĢĐĢŽ
m+3Ģ―0ĢŽ―âĩÃmĢ―Đ2ŧō1ĢĻÉáČĨĢĐĢŽ
ĄāEĢĻĐ2ĢŽ2ĢĐĢŽ
ĄßAĢĻĐ3ĢŽ0ĢĐĄĒBĢĻ2ĢŽ0ĢĐĢŽ
ĄāABĢ―5ĢŽAEĢ―![]() ĢŽBEĢ―2
ĢŽBEĢ―2![]() ĢŽ
ĢŽ
ĄāAB2Ģ―AE2+BE2ĢŽ
ĄāĄÏAEBĢ―ĄÏDOBĢ―90ĄãĢŽ
ĄāĄÏEAB+ĄÏEBAĢ―ĄÏODB+ĄÏEBAĢ―90ĄãĢŽ
ĄāĄÏEABĢ―ĄÏODBĢŽ
ĢĻĒņĢĐĩąĄũFEAĄŨĄũBODĘąĢŽ
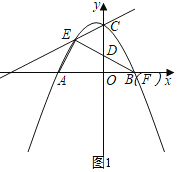
ĄāĄÏAEFĢ―ĄÏDOBĢ―90ĄãĢŽ
ĄāFÓëBĩãÖØšÏĢŽ
ĄāEFĢ―BEĢ―2![]() ĢŽ
ĢŽ
ĢĻĒōĢĐĩąĄũEFAĄŨĄũBODĘąĢŽ
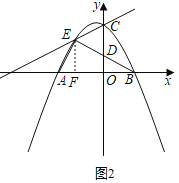
ĄāĄÏAFEĢ―ĄÏDOBĢ―90ĄãĢŽ
ĄßEĢĻĐ2ĢŽ2ĢĐĢŽ
ĄāEFĢ―2ĢŽ
đĘĢšEFĩÄģĪΊ2![]() ŧō2Ģŧ
ŧō2Ģŧ
ĒÚĩã![]() ĩÄŨøąęΊ
ĩÄŨøąęΊ![]() ĢŽ
ĢŽ![]() ŧō
ŧō![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ĢĻĒņĢĐđýĩãHŨũHNĄÍCOÓÚĩãNĢŽđýĩãGŨũGMĄÍHNÓÚĩãMĢŽ
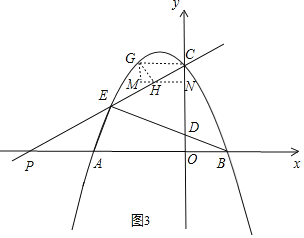
ĄāĄÏGMNĢ―ĄÏCNHĢ―90ĄãĢŽ
ÓÖĄÏGHCĢ―90ĄãĢŽ
ĄāĄÏCHN+ĄÏGHMĢ―ĄÏMGH+ĄÏGHMĢ―90ĄãĢŽ
ĄāĄÏCHNĢ―ĄÏMGHĢŽ
ĄßHNĄÍCOĢŽĄÏCOPĢ―90ĄãĢŽ
ĄāHNĄÎABĢŽ
ĄāĄÏCHNĢ―ĄÏAPEĢ―ĄÏMGHĢŽ
ĄßEĢĻĐ2ĢŽ2ĢĐĢŽCĢĻ0ĢŽ3ĢĐĢŽ
ĄāÖąÏßCEĩÄ―âÎöĘ―ÎŠyĢ―![]() x+3ĢŽ
x+3ĢŽ
ĄāPĢĻĐ6ĢŽ0ĢĐĢŽ
ĄāEPĢ―EBĢ―2![]() ĢŽ
ĢŽ
ĄāĄÏAPEĢ―ĄÏEBAĢŽ
ĄßĄÏGCHĢ―ĄÏEBAĢŽ
ĄāĄÏGCHĢ―ĄÏAPEĢ―ĄÏEBAĢ―ĄÏCHNĢ―ĄÏMGHĢŽ
ĄāGCĄÎPBĢŽ
ÓÖCĢĻ0ĢŽ3ĢĐĢŽ
ĄāGĩãĩÄŨÝŨøąęΊ3ĢŽīúČëyĢ―Đ![]() x+3ÖÐĢŽĩÃĢšxĢ―Đ1ŧō0ĢĻÉáČĨĢĐĢŽ
x+3ÖÐĢŽĩÃĢšxĢ―Đ1ŧō0ĢĻÉáČĨĢĐĢŽ
ĄāMNĢ―1ĢŽ
ĄßĄÏAEBĢ―90ĄãĢŽAEĢ―![]() ĢŽBEĢ―2
ĢŽBEĢ―2![]() ĢŽ
ĢŽ
ĄātanĄÏEBAĢ―tanĄÏCHNĢ―tanĄÏMGHĢ―![]() ĢŽ
ĢŽ
ÉčCNĢ―MGĢ―mĢŽÔōHNĢ―2mĢŽMHĢ―![]() mĢŽ
mĢŽ
ĄāMH+HNĢ―2m+![]() mĢ―1ĢŽ
mĢ―1ĢŽ
―âĩÃĢŽmĢ―![]() ĢŽ
ĢŽ
ĄāHĩãĩÄMŨøąęΊĐ![]() ĢŽīúČëyĢ―
ĢŽīúČëyĢ―![]() x+3ĢŽĩÃĢšyĢ―
x+3ĢŽĩÃĢšyĢ―![]() ĢŽ
ĢŽ
ĄāĩãHĩÄŨøąęΊĢĻĐ![]() ĢŽ
ĢŽ![]() ĢĐĢŪ
ĢĐĢŪ
ĢĻĒōĢĐđýĩãHŨũMNĄÍPBĢŽđýĩãCŨũCNĄÍMHÓÚĩãNĢŽđýĩãGŨũGMĄÍHMÓÚĩãMĢŽ
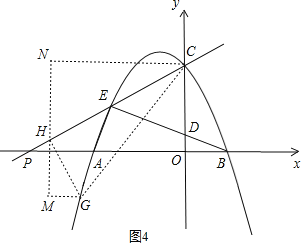
ĄāCNĄÎPBĢŽ
ĄāĄÏNCHĢ―ĄÏAPEĢŽ
ÓÉĢĻĒņĢĐÖŠĢšĄÏAPEĢ―ĄÏEBAĢŽÔōĄÏNCHĢ―ĄÏEBAĢŽ
ĄßĄÏGMNĢ―ĄÏCNHĢ―90ĄãĢŽ
ÓÖĄÏGHCĢ―90ĄãĢŽ
ĄāĄÏHCN+ĄÏNHCĢ―ĄÏMHG+ĄÏNHCĢ―90ĄãĢŽ
ĄāĄÏHCNĢ―ĄÏMHGĢŽ
ĄßĄÏGCHĢ―ĄÏEBAĢŽ
ĄāĄÏGCHĢ―ĄÏEBAĢ―ĄÏHCNĢ―ĄÏMHGĢŽ
ÓÉĢĻĒņĢĐÖŠĢš![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
ÓÖ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
ÓÉĢĻĒņĢĐÖŠĢš![]() ĢŽ
ĢŽ
Ôō![]() ĢŽ
ĢŽ
Éč![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
![]()
![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ![]() ĢŽÓÖ
ĢŽÓÖ![]() ĢŽ
ĢŽ
![]() ĢŽīúČë
ĢŽīúČë![]() ÖÐĢŽĩÃĢŽ
ÖÐĢŽĩÃĢŽ![]() ŧō0ĢĻÉáČĨĢĐĢŽ
ŧō0ĢĻÉáČĨĢĐĢŽ
![]() ĢŽ
ĢŽ
![]() ĩãĩÄMŨøąęΊ
ĩãĩÄMŨøąęΊ![]() ĢŽīúČë
ĢŽīúČë![]() ĢŽĩÃĢŽ
ĢŽĩÃĢŽ![]() ĢŪ
ĢŪ
![]() ĩã
ĩã![]() ĩÄŨøąęΊ
ĩÄŨøąęΊ![]() ĢŪ
ĢŪ
ŨÛšÏŌÔÉÏŋÉĩÃĩã![]() ĩÄŨøąęΊ
ĩÄŨøąęΊ![]() ĢŽ
ĢŽ![]() ŧō
ŧō![]() ĢŪ
ĢŪ


 ÄÜŋžĘÔÆÚÄĐģåīĖūíÏĩÁÐīð°ļ
ÄÜŋžĘÔÆÚÄĐģåīĖūíÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽūØÐÎABCDÖÐĢŽAB=3ĢŽBC=4ĢŽķŊĩãPīÓAĩãģö·ĒĢŽ°īAĄúBĄúCĩÄ·―ÏōÔÚABšÍBCÉÏŌÆķŊĢŽžĮPA=xĢŽĩãDĩ―ÖąÏßPAĩÄūāĀëΊyĢŽÔōyđØÓÚxĩÄšŊĘýÍžÏóīóÖÂĘĮĢĻ ĢĐ
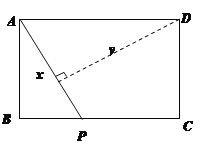
A.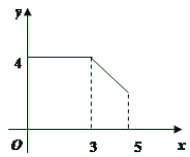 B.
B.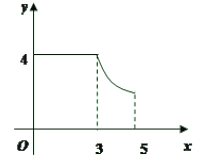
C.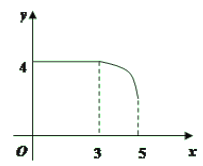 D.
D.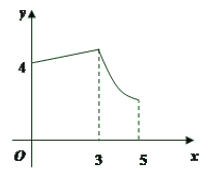
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÐÂđÚ·ÎŅŨŌßĮéÆÚžäĢŽÄģÐĄĮøžÆŧŪđšÂōžŨĄĒŌŌÁ―ÖÖÆ·ÅÆĩÄÏûķūžÁĢŽŌŌÆ·ÅÆÏûķūžÁÃŋÆŋĩÄžÛļņąČžŨÆ·ÅÆÏûķūžÁÃŋÆŋžÛļņĩÄ3ąķÉŲ50ÔŠĢŽŌŅÖŠÓÃ300ÔŠđšÂōžŨÆ·ÅÆÏûķūžÁĩÄĘýÁŋÓëÓÃ400ÔŠđšÂōŌŌÆ·ÅÆÏûķūžÁĩÄĘýÁŋÏāÍŽĢŪ
(1)ĮóžŨĄĒŌŌÁ―ÖÖÆ·ÅÆÏûķūžÁÃŋÆŋĩÄžÛļņļũĘĮķāÉŲÔŠĢŋ
(2)ČôļÃÐĄĮøīÓģŽĘÐŌŧīÎÐÔđšÂōžŨĄĒŌŌÁ―ÖÖÆ·ÅÆĩÄÏûķūžÁđē40ÆŋĢŽĮŌŨÜ·ŅÓÃΊ1400ÔŠĢŽĮóđšÂōÁËķāÉŲÆŋŌŌÆ·ÅÆÏûķūžÁĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģÐĢūŲÐÐĄ°ššŨÖĖýÐīĄąąČČüĢŽÃŋÎŧŅ§ÉúĖýÐīššŨÖ40ļöĢŽąČČü―áĘøšóËæŧúģéēéēŋ·ÖŅ§ÉúĖýÐīĄ°ÕýČ·ĩÄŨÖĘýĄąĢŽŌÔÏÂĘĮļųūÝģéēé―áđûŧæÖÆĩÄÍģžÆÍžąíĢŪ
ÆĩĘý·Öēžąí
Ũéąð | ÕýČ·ĩÄŨÖĘý | ČËĘý |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
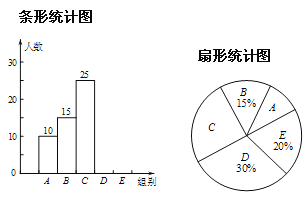
ļųūÝŌÔÉÏÐÅÏĒ―âūöÏÂÁÐÎĘĖâĢš
ĢĻ1ĢĐēđČŦĖõÐÎÍģžÆÍžĢŧ
ĢĻ2ĢĐÉČÐÎÍģžÆÍžÖÐĄ°![]() Ũ饹ËųķÔÓĶĩÄÔēÐÄ―ĮĩÄķČĘýĘĮ_________Ģŧ
Ũ饹ËųķÔÓĶĩÄÔēÐÄ―ĮĩÄķČĘýĘĮ_________Ģŧ
ĢĻ3ĢĐČôļÃÐĢđēÓÐ1210ÃûŅ§ÉúĢŽČįđûĖýÐīÕýČ·ĩÄŨÖĘýÉŲÓÚ25ĢŽÔōķĻΊēŧšÏļņĢŧĮëÄãđĀžÆÕâËųŅ§ÐĢąūīÎąČČüĖýÐīēŧšÏļņĩÄŅ§ÉúČËĘýĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚĩȹߥũABCÄÚČÎČĄŌŧĩãDĢŽÁŽ―ÓCDĢŽBDĩÃĩ―ĄũCDBĢŽČįđûĩȹߥũABCÄÚÃŋŌŧĩãąŧČĄĩ―ĩÄŋÉÄÜÐÔķžÏāÍŽĢŽÔōĄũCBDĘĮķÛ―ĮČý―ĮÐÎĩÄļÅÂĘĘĮ______ĢŪ
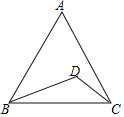
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋΊÁË―âļßÐĢŅ§ÉúķÔ5GŌÆķŊÍĻÐÅÍøÂįĩÄÏû·ŅŌâÔļĢŽīÓÔÚÐĢīóŅ§ÉúÖÐËæŧúģéČĄÁË1000ČË―øÐÐĩũēéĢŽÏÂÃæĘĮīóŅ§ÉúÓÃŧ§·ÖĀāĮéŋöÍģžÆąíšÍīóŅ§ÉúÔļŌâΊ5GĖŨēÍķāÖ§ļķĩÄ·ŅÓÃĮéŋöÍģžÆÍžĢĻĀýČįĢŽÔįÆÚĖåŅéÓÃŧ§ÖÐÔļŌâΊ5GĖŨēÍķāÖ§ļķ10ÔŠĩÄČËĘýÕžËųÓÐÔįÆÚĖåŅéÓÃŧ§ĩÄ50%ĢĐĢŪ
ÓÃŧ§·ÖĀā | ČËĘý |
AĢšÔįÆÚĖåŅéÓÃŧ§ĢĻÄŋĮ°ŌŅÉýžķΊ5GÓÃŧ§ĢĐ | 260ČË |
BĢšÖÐÆÚļúËæÓÃŧ§ĢĻŌŧÄęÄÚ―ŦÉýžķΊ5GÓÃŧ§ĢĐ | 540ČË |
CĢššóÆÚÓÃŧ§ĢĻŌŧÄęšóēÅÉýžķΊ5GÓÃŧ§ĢĐ | 200ČË |
ÏÂÁÐÍÆķÏÖÐĢŽēŧšÏĀíĩÄĘĮĢĻ ĢĐ

A.ÔįÆÚĖåŅéÓÃŧ§ÖÐĢŽÔļŌâΊ5GĖŨēÍķāÖ§ļķ10ÔŠĢŽ20ÔŠĢŽ30ÔŠĩÄČËĘýŌĀīÎĩÝžõ
B.šóÆÚÓÃŧ§ÖÐĢŽÔļŌâΊ5GĖŨēÍķāÖ§ļķ20ÔŠĩÄČËĘýŨîķā
C.ÔļŌâΊ5GĖŨēÍķāÖ§ļķ10ÔŠĩÄÓÃŧ§ÖÐĢŽÖÐÆÚļúËæÓÃŧ§ČËĘýŨîķā
D.ÔļŌâΊ5GĖŨēÍķāÖ§ļķ20ÔŠĩÄÓÃŧ§ÖÐĢŽšóÆÚÓÃŧ§ČËĘýŨîķā
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽ°ëÔēOĩÄÖąūķABĢ―6cmĢŽĩãMÔÚÏßķÎABÉÏĢŽĮŌBMĢ―1cmĢŽĩãPĘĮ![]() ÉÏĩÄķŊĩãĢŽđýĩãAŨũANĄÍÖąÏßPMĢŽīđŨãΊĩãNĢŪ
ÉÏĩÄķŊĩãĢŽđýĩãAŨũANĄÍÖąÏßPMĢŽīđŨãΊĩãNĢŪ

ÐĄķŦļųūÝŅ§Ï°šŊĘýĩÄūŅéĢŽķÔÏßķÎANĢŽMNĢŽPMĩÄģĪķČÖŪžäĩÄđØÏĩ―øÐÐÁËĖ―ūŋĢŪÏÂÃæĘĮÐĄķŦĩÄĖ―ūŋđýģĖĢŽĮëēđģäÍęÕûĢš
ĢĻ1ĢĐķÔÓÚĩãPÔÚ![]() ÉÏĩÄēŧÍŽÎŧÖÃĢŽŧÍžĄĒēâÁŋĢŽĩÃĩ―ÁËÏßķÎANĢŽMNĢŽPMĩÄģĪķČĩÄžļŨéÖĩĢŽČįąíĢš
ÉÏĩÄēŧÍŽÎŧÖÃĢŽŧÍžĄĒēâÁŋĢŽĩÃĩ―ÁËÏßķÎANĢŽMNĢŽPMĩÄģĪķČĩÄžļŨéÖĩĢŽČįąíĢš
ÎŧÖÃ1 | ÎŧÖÃ2 | ÎŧÖÃ3 | ÎŧÖÃ4 | ÎŧÖÃ5 | ÎŧÖÃ6 | ÎŧÖÃ7 | |
AN/cm | 0.00 | 3.53 | 4.58 | 5.00 | 4.58 | 4.00 | 0.00 |
MN/cm | 5.00 | 3.53 | 2.00 | 0.00 | 2.00 | 3.00 | 5.00 |
PM/cm | 1.00 | 1.23 | 1.57 | 2.24 | 3.18 | 3.74 | 5.00 |
ÔÚANĢŽMNĢŽPMĩÄģĪķČÕâČýļöÁŋÖÐĢŽČ·ķĻĄĄ ĄĄĩÄģĪķČĘĮŨÔąäÁŋĢŽĄĄ ĄĄšÍĄĄ ĄĄĩÄģĪķČķžĘĮÕâļöŨÔąäÁŋĩÄšŊĘýĢŧ
ĢĻ2ĢĐÔÚÍŽŌŧÆ―ÃæÖą―ĮŨøąęÏĩxOyÖÐĢŽŧģöĢĻ1ĢĐÖÐËųČ·ķĻĩÄšŊĘýĩÄÍžÏóĢŧ
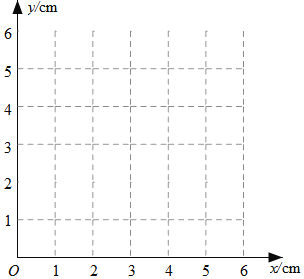
ĢĻ3ĢĐ―ášÏšŊĘýÍžÏóĢŽ―âūöÎĘĖâĢšĩąANĢ―MNĘąĢŽPMĩÄģĪķČԞΊĄĄ ĄĄcmĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
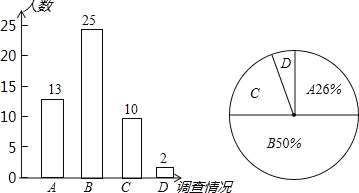
ĄūĖâÄŋĄŋ2015Đ2016ÄęCBAÁŠČüĢŽžŠÁÖūÅĖĻÅĐÉĖÐÐķÓ°ŅģĪīšĖåÓýđÝŨũΊŨÔžšĩÄÖũģĄĢŽÐĄĮōÃÔĄ°ĮōĮōĄąķÔŨÔžšŅ§ÐĢēŋ·ÖŅ§ÉúķÔČĨČüģĄÎŠĮōķÓžÓÓÍÖúÍþ―øÐÐÁËģéŅųĩũēéĢŽļųūÝĘÕžŊĩ―ĩÄĘýūÝŧæÖÆÁËČįÏÂĩÄÍģžÆÍžąíĢŪĢĻĩũēéĮéŋöËĩÃũĢšAĢšĖØąðÔļŌâČĨĢŧBĢšÔļŌâČĨĢŧCĢšČĨēŧČĨķžÐÐĢŧDĢšēŧÔļŌâČĨĢĐ
ĢĻ1ĢĐĮóģöēŧÔļŌâČĨĩÄŅ§ÉúĩÄČËĘýÕžąŧĩũēéŨÜČËĘýĩÄ°Ų·ÖąČĢŧ
ĢĻ2ĢĐĮóģöÉČÐÎÍģžÆÍžÖÐCËųÔÚĩÄÉČÐÎÔēÐÄ―ĮĩÄķČĘýĢŧ
ĢĻ3ĢĐČôļÃÐĢŅ§ÉúđēÓÐ2000ČËĢŽĮëÄãđĀžÆĖØąðÔļŌâČĨžÓÓÍÖúÍþĩÄŅ§ÉúđēÓÐķāÉŲČËĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔËÓÃÓïŌôĘķąðĘäČëÍģžÆŋÉŌÔĖáļßÎÄŨÖĘäČëĩÄËŲķČĢŽÎŠÁË―âAĢŽBÁ―ÖÖÓïŌôĘķąðĘäČëČížþĩÄŋÉķÁÐÔĢŽÐĄĮØÍŽŅ§ËæŧúŅĄÔņÁË20ķÎŧ°ĢŽÆäÖÐÃŋķÎŧ°ķžšŽÓÐ100ļöŨÖ(ēŧžÆąęĩã·ûšÅ)ĢŽÔÚąĢģÖÏāÍŽĖõžþÏÂĢŽąęŨžÆÕÍĻŧ°ĀīēâĘÔÁ―ÖÖÓïŌôĘķąðĘäČëČížþĩÄŨžČ·ÐÔĢŽÕûļöēâĘÔ·ÖÎöđýģĖČįÏÂĢŽĮëēđģäÍęÕûĢŪ
(1)ĘÕžŊĘýūÝĢšÁ―ÖÖČížþÃŋīÎĘķąðÕýČ·ĩÄŨÖĘýžĮžČįÏÂĢš

(2)ÕûĀíĢŽÃčĘöĘýūÝĢšļųūÝÉÏÃæĩÃĩ―ĩÄÁ―ŨéŅųąūĘýūÝĢŽŧæÖÆÁË·ÖēžÖą·―Íž
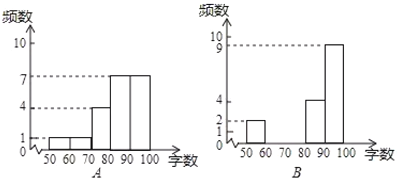
(3)·ÖÎöĘýūÝĢšÁ―ŨéŅųąūĘýūÝĩÄÆ―ūųĘýĢŽÖÚĘýĢŽÖÐÎŧĘýĢŽ·―ēîČįÏÂąíËųĘū
Æ―ūųĘý | ÖÚĘý | ÖÐÎŧĘý | ·―ēî | |
A | 84.7 | 84.5 | 88.91 | |
B | 83.7 | 96 | 184.01 |
(4)ĩÃģö―áÂÛĢšļųūÝŌÔÉÏÐÅÏĒĢŪÅÐķÏ____ÖÖÓïŌôĘķąðĘäČëČížþĩÄŨžČ·ÐÔ―ÏšÃĢŽĀíÓÉČįÏÂĢŪ_______________(ÖÁÉŲīÓÁ―ļöēŧÍŽĩÄ―ĮķČËĩÃũÅÐķÏĩÄšÏĀíÐÔ) ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com