
【题目】某校举办球赛,分为若干组,其中第一组有A,B,C,D,E五个队.这五个队要进行单循环赛,即每两个队之间要进行一场比赛,每场比赛采用三局两胜制,即三局中胜两局就获胜.每场比赛胜负双方根据比分会获得相应的积分,积分均为正整数.这五个队完成所有比赛后得到如下的积分表.
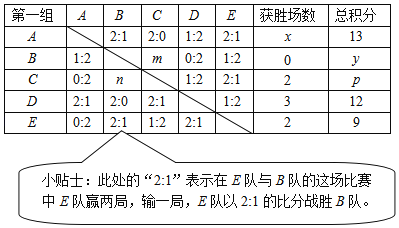
根据上表回答下列问题:
(1)第一组一共进行了 场比赛,A队的获胜场数x为 ;
(2)当B队的总积分y=6时,上表中m处应填 ,n处应填 ;
(3)写出C队总积分p的所有可能值为: .
【答案】(1)10,3;(2)0:2, 2:0;(3)9或10
【解析】
(1)按照5个队中每个队都要和另外4个队进行一场比赛,而A与B和B与A属于同一场比赛,列式计算或直接从表中数一下即可得比赛场数;根据表中比赛结果可直接得出A队的获胜场数x的值;
(2)每场比赛的结果有四种:0:2,1:2,2:1,2:0,设以上四种得分为a,b,c,d,且a<b<c<d,根据E和A的总分可得关于a,b,c,d的等式,化简即可得出a,b,c,d的值,设m对应的积分为x,根据题意得关于x的方程,解得x的值,则可得答案;
(3)C队胜2场,分两种情况:当C、B的结果为2:0时;当C、B的结果为2:1时,分别计算出p的值即可.
解:(1)∵![]() (场),
(场),
∴第一组一共进行了10场比赛;
∵每场比赛采用三局两胜制,A、B的结果为2:1,A、C的结果为2:0,A、E的结果为2:0,
∴A队的获胜场数x为3;
故答案为:10,3;
(2)由题可知:每场比赛的结果有四种:0:2,1:2,2:1,2:0,
根据题意可知每种结果都会得到一个正整数积分,设以上四种得分为a,b,c,d,且a<b<c<d,
根据E的总分可得:a+c+b+c=9,
∴a=1,b=2,c=3,
根据A的总分可得:c+d+b+d=13,
∴d=4,
设m对应的积分为x,
当y=6时,b+x+a+b=6,即2+x+1+2=6,
∴x=1,
∴m处应填0:2;
∴B:C=0:2,
∴C:B=2:0,
∴n处应填2:0;
(3)∵C队胜2场,
∴分两种情况:当C、B的结果为2:0时,
p=1+4+3+2=10;
当C、B的结果为2:1时,
p=1+3+3+2=9;
∴C队总积分p的所有可能值为9或10.
故答案为:9或10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众志成城,抗击疫情,救助重灾区.某校某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):100,45,100,40,100,60,155.下面有四个推断:
①这7名同学所捐的零花钱的平均数是150;
②这7名同学所捐的零花钱的中位数是100;
③这7名同学所捐的零花钱的众数是100;
④由这7名同学所捐的零花钱的中位数是100,可以推断该校全体同学所捐的零花钱的中位数也一定是100.
所有合理推断的序号是( )
A.①③B.②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月,胡润研究院携手知识产权与科创云平台汇桔,联合发布《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》,白皮书公布了2019中国人工智能企业知识产权竞争力百强榜,对500余家中国人工智能主流企业进行定量评估(满分100分),前三名分别为:华为、腾讯、百度.对得分由高到低的前41家企业的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.得分的频数分布直方图:
(数据分成8组:60≤x<65,65≤x<70,70≤x<75,75≤x<80,80≤x<85,85≤x<90,90≤x<95,95≤x≤100,)
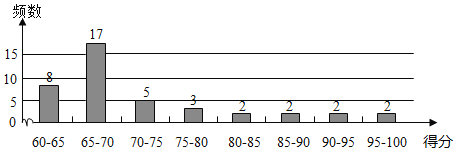
b.知识产权竞争力得分在70≤x<75这一组的是:70.3,71.6,72.1,72.5,74.1.
c.41家企业注册所在城市分布图(不完整)如图:(结果保留一位小数)
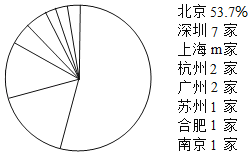
d.汉王科技股份有限公司的知识产权竞争力得分是70.3.
(以上数据来源于《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》)
根据以上信息,回答下列问题:
(1)汉王科技股份有限公司的知识产权竞争力得分排名是第 ;
(2)百度在人工智能领域取得诸多成果,尤其在智能家居、自动驾驶与服务于企业的智能云领域,百度都已进行前瞻布局,请你估计百度在本次排行榜中的得分大概是 ;
(3)在41家企业注册所在城市分布图中,m= ,请用阴影标出代表上海的区域;
(4)下列推断合理的是 .(只填序号)
①前41家企业的知识产权竞争力得分的中位数应在65≤x<70这一组中,众数在65≤x<70这一组的可能性最大;
②前41家企业分布于我国8个城市.人工智能产业的发展聚集于经济、科技、教育相对发达的城市,一线城市中,北京的优势尤其突出,贡献榜单过半的企业,充分体现北京在人工智能领域的产业集群优势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果四边形有一组对边平行,且另一组对边不平行,那么称这样的四边形为梯形,若梯形中有一个角是直角,则称其为直角梯形.下面四个结论中:
①存在无数个直角梯形,其四个顶点分别在同一个正方形的四条边上;
②存在无数个直角梯形,其四个顶点在同一条抛物线上;
③存在无数个直角梯形,其四个顶点在同一个反比例函数的图象上;
④至少存在一个直角梯形,其四个顶点在同一个圆上.
所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
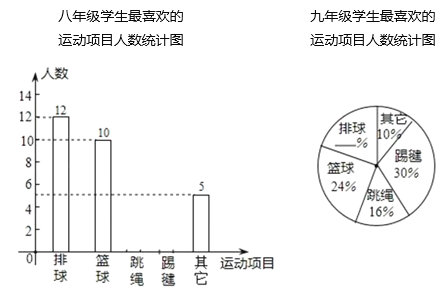
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
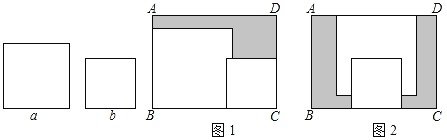
A.aB.bC.ADD.AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是我国建国70周年,回顾过去展望未来,创新是引领发展的第一动力,北京科技创新能力不断增强,下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况.
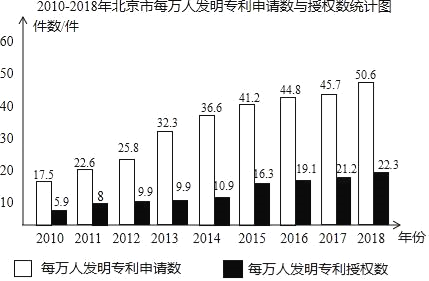
根据统计图提供的信息,下列推断合理的是( )
A. 2010﹣2018年,北京市毎万人发明专利授权数逐年增长
B. 2010﹣2018年,北京市毎万人发明专利授权数的平均数超过10件
C. 2010年申请后得到授权的比例最低
D. 2018年申请后得到授权的比例最高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
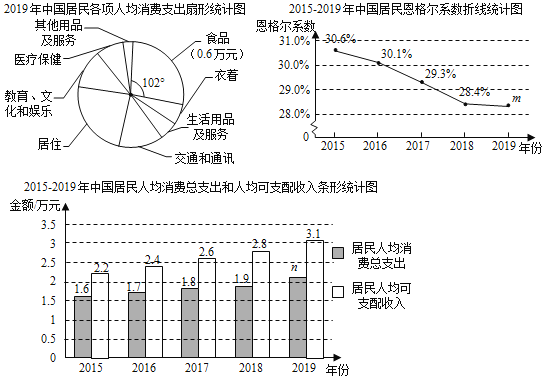
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com