
【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
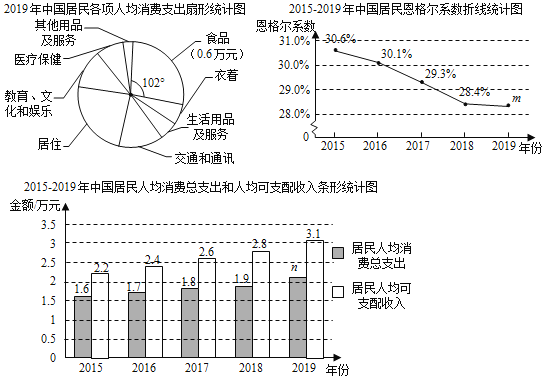
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
【答案】(1)28.3%;(2)2.1;(3)①②.
【解析】
(1)根据扇形统计图中食品所占的圆心角的度数÷360°即可得到结论;
(2)根据食品支出占消费总支出的百分比×0.6即可得到结论;
(3)由折线统计图和条形统计图中的信息监控得到结论.
解:(1)2019年中国城乡居民恩格尔系数m约为![]() ×100%≈28.3%,
×100%≈28.3%,
故答案为:28.3%;
(2)2019年居民人均消费总支出n约为0.6÷28.3%≈2.1(万元);
(3)由条形统计图可以看出2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
由折线统计图可知2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
故推断合理的是①②;
故答案为:(1)28.3%;(2)2.1;(3)①②.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】某校举办球赛,分为若干组,其中第一组有A,B,C,D,E五个队.这五个队要进行单循环赛,即每两个队之间要进行一场比赛,每场比赛采用三局两胜制,即三局中胜两局就获胜.每场比赛胜负双方根据比分会获得相应的积分,积分均为正整数.这五个队完成所有比赛后得到如下的积分表.
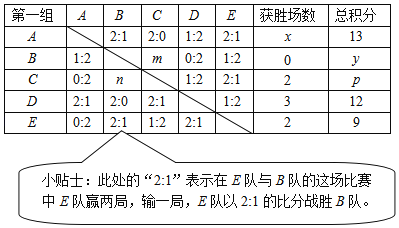
根据上表回答下列问题:
(1)第一组一共进行了 场比赛,A队的获胜场数x为 ;
(2)当B队的总积分y=6时,上表中m处应填 ,n处应填 ;
(3)写出C队总积分p的所有可能值为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.
(1)已知点A(4,0);
①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;
②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x﹣5上,则点B的坐标为 ;
(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
(1)求k及点B的坐标;
(2)若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上存在点P、点M与线段AB.若线段AB上存在一点Q,使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.
已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
(1)在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是 ;
(2)点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;
(3)已知点M(m,﹣1),若直线y=![]() x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质并解决问题.
的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)取几组![]() 与
与![]() 的对应值,填写在下表中.
的对应值,填写在下表中.
| … |
|
|
| 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
| … | 1 | td style="width:6%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 |
| 1.5 | 1 | … |
![]() 的值为_____________;
的值为_____________;
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
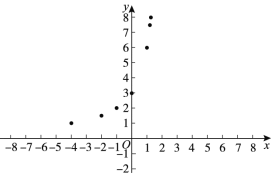
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数![]() 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;
②过点![]() 作直线
作直线![]() 轴,与函数
轴,与函数![]() 的图象交于点
的图象交于点![]() (点
(点![]() 在点
在点![]() 的左侧),则
的左侧),则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
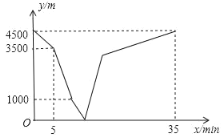
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(x1,y1),(x2,y2),且x1≤x2,d=|y1-y2|.将这个函数图象在直线y=y1下方部分沿直线y=y1翻折,并将其向上平移d个单位,将这部分图象与原函数图象剩余部分的图象组成的新图象记为G,图象G对应的函数叫做这个函数的伴随函数.例如:点A(1,0)、B(2,1)在一次函数y=x-1的图象上,则它的伴随函数为![]() .
.
(1)点A、B在直线y=-2x上,点A在第二象限,点B在x轴上.当d=2时,求函数y=-2x的伴随函数所对应的函数表达式.
(2)二次函数y=x2-2x-3的图象交x轴负半轴交于点A,点B在抛物线上,设点B的横坐标为m.
①当d=0时,求该抛物线的伴随函数的图象G与直线y=4在第一象限的交点坐标;
②若直线y=2与该抛物线的伴随函数的图象G有四个交点,直接写出m的取值范围.
(3)抛物线y=x2-2nx+n2-n-1与y轴交于点A,点B在点A的左侧抛物线上,且d=1,当该抛物线的伴随函数的图象G上的点到x轴距离的最小值为1时,直接写出n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com