
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
【答案】(1)⊙B,⊙C;(2)1≤t≤2+![]() ;(3)60°≤∠EOM<90°
;(3)60°≤∠EOM<90°
【解析】
(1)画出图象,根据角内相切圆的定义判断即可.
(2)求出两种特殊位置时t的值即可判断.
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆.
)的圆为∠EMO的角内相切圆.
(1)如图1中,观察图象可知,⊙B和⊙C,其中是∠EOF的角内圆.
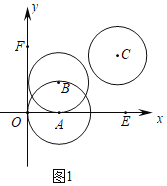
故答案为:⊙B,⊙C.
(2)解:如图,
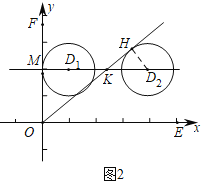
当⊙D1与y轴相切时,设切点为M,则MD1=1,可得t1=1.
当⊙D2与y=x相切时,设切点为H,连接HD2,设直线y=x与直线y=2交于点K,则△HKD2,△MOK都是等腰直角三角形,
∵KH=HD2=1,
∴KD2=![]() ,
,
∵OM=MK=2,
∴MD2=MK+KD2=2+![]()
可得t2=2+![]() ,
,
观察图象可知,满足条件的t的取值范围是1≤t≤2+![]() .
.
(3)如图3中,连接OP,OM.
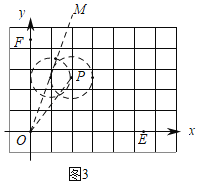
∵P(2,2![]() ),
),
∴tan∠POE=![]() =
=![]() ,
,
∴∠POE=60°,
观察图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,
)的圆为∠EMO的角内相切圆,
∴60°≤∠EOM<90°.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
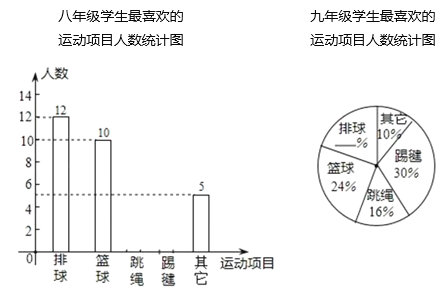
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
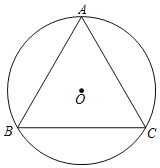
【题目】如图,等边△ABC,作它的外接圆⊙O,连接AO并延长交⊙O于点D,交BC于点E,过点D作DF∥BC,交AC的延长线于点F.
(1)依题意补全图形并证明:DF与⊙O相切;
(2)若AB=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P.
(1)过点P作与x轴平行的直线,交抛物线于点Q,PQ=4,求![]() 的值;
的值;
(2)横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W.若区域W内恰有4个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出比重越低,居民家庭越富裕,反之越贫穷.
下面是根据从权威机构获得的部分数据绘制的统计图:
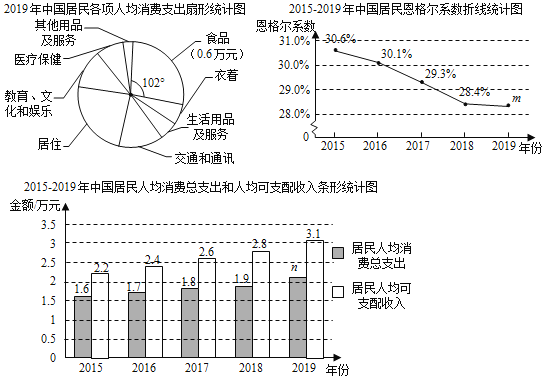
根据以上信息,回答下列问题:
(1)2019年中国城乡居民恩格尔系数m约为 (精确到0.1%);
(2)2019年居民人均消费总支出n约为 万元(精确到千位);
(3)下面的推断合理的是 .
①2015﹣2019年中国城乡居民人均可支配收入和人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015﹣2019年中国城乡居民恩格尔系数呈现下降趋势,说明中国居民家庭富裕程度越来越高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先进制造业城市发展指数是反映一个城市先进制造水平的综合指数.对2019年我国先进制造业城市发展指数得分排名位居前列的30个城市的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.先进制造业城市发展指数得分的频数分布直方图(数据分成6组:![]() ):
):
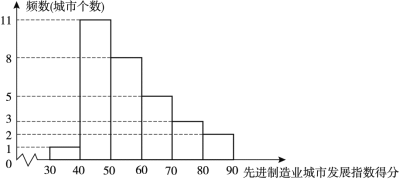
b.先进制造业城市发展指数得分在![]() 这一组的是:71.1 75.7 79.9
这一组的是:71.1 75.7 79.9
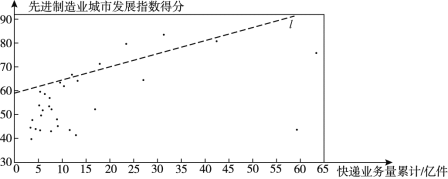
c.30个城市的2019年快递业务量累计和先进制造业城市发展指数得分情况统计图:
d.北京的先进制造业城市发展指数得分为79.9.
根据以上信息,回答下列问题:
(1)在这30个城市中,北京的先进制造业城市发展指数排名第![]() ;
;
(2)在30个城市的快递业务量累计和先进制造业城市发展指数得分情况统计图中,包括北京在内的少数几个城市所对应的点位于虚线![]() 的上方.请在图中用“○”圈出代表北京的点;
的上方.请在图中用“○”圈出代表北京的点;
(3)在这30个城市中,先进制造业城市发展指数得分高于北京的城市的快递业务量累计的最小值约为_______亿件.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,市场上防护口罩出现热销.某药店用![]() 元购进甲,乙两种不同型号的口罩共
元购进甲,乙两种不同型号的口罩共![]() 个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的
个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的![]() 倍.
倍.
![]() 求购进的甲,乙两种口罩的单价各是多少?
求购进的甲,乙两种口罩的单价各是多少?
![]() 若甲,乙两种口罩的进价不变,该药店计划用不超过
若甲,乙两种口罩的进价不变,该药店计划用不超过![]() 元的资金再次购进甲,乙两种口罩共
元的资金再次购进甲,乙两种口罩共![]() 个,求甲种口罩最多能购进多少个?
个,求甲种口罩最多能购进多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com