
【题目】在抗击新冠肺炎疫情期间,市场上防护口罩出现热销.某药店用![]() 元购进甲,乙两种不同型号的口罩共
元购进甲,乙两种不同型号的口罩共![]() 个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的
个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的![]() 倍.
倍.
![]() 求购进的甲,乙两种口罩的单价各是多少?
求购进的甲,乙两种口罩的单价各是多少?
![]() 若甲,乙两种口罩的进价不变,该药店计划用不超过
若甲,乙两种口罩的进价不变,该药店计划用不超过![]() 元的资金再次购进甲,乙两种口罩共
元的资金再次购进甲,乙两种口罩共![]() 个,求甲种口罩最多能购进多少个?
个,求甲种口罩最多能购进多少个?
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
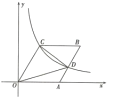
【题目】如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数![]() 的图象与AB交于点D,则△COD的面积为( )
的图象与AB交于点D,则△COD的面积为( )
A.![]() B.
B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(x1,y1),(x2,y2),且x1≤x2,d=|y1-y2|.将这个函数图象在直线y=y1下方部分沿直线y=y1翻折,并将其向上平移d个单位,将这部分图象与原函数图象剩余部分的图象组成的新图象记为G,图象G对应的函数叫做这个函数的伴随函数.例如:点A(1,0)、B(2,1)在一次函数y=x-1的图象上,则它的伴随函数为![]() .
.
(1)点A、B在直线y=-2x上,点A在第二象限,点B在x轴上.当d=2时,求函数y=-2x的伴随函数所对应的函数表达式.
(2)二次函数y=x2-2x-3的图象交x轴负半轴交于点A,点B在抛物线上,设点B的横坐标为m.
①当d=0时,求该抛物线的伴随函数的图象G与直线y=4在第一象限的交点坐标;
②若直线y=2与该抛物线的伴随函数的图象G有四个交点,直接写出m的取值范围.
(3)抛物线y=x2-2nx+n2-n-1与y轴交于点A,点B在点A的左侧抛物线上,且d=1,当该抛物线的伴随函数的图象G上的点到x轴距离的最小值为1时,直接写出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东日照)已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )

A. ①②③ B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
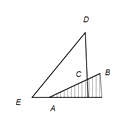
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)![]() =1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:
=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:![]() °≈0.73,cos8°≈0.67,tan48°≈1.11)
°≈0.73,cos8°≈0.67,tan48°≈1.11)
A.17.0米B.21.9米C.23.3米D.33.3米
查看答案和解析>>
科目:初中数学 来源: 题型:
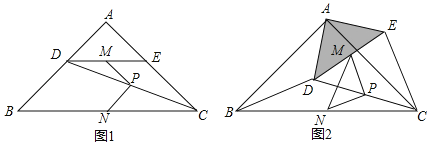
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com