
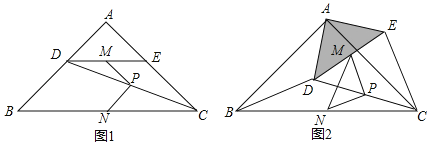
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎRtΓςABC÷–Θ§ΓœAΘΫ90ΓψΘ§ABΘΫACΘ§ΒψDΘ§EΖ÷±π‘Ύ±ΏABΘ§AC…œΘ§ADΘΫAEΘ§Ν§Ϋ”DCΘ§ΒψMΘ§PΘ§NΖ÷±πΈΣDEΘ§DCΘ§BCΒΡ÷–ΒψΘ°
Θ®1Θ©Ιέ≤λ≤¬œκΘΚΆΦ1÷–Θ§œΏΕΈPM”κPNΒΡ ΐΝΩΙΊœΒ «ΓΓ ΓΓΘ§ΈΜ÷ΟΙΊœΒ «ΓΓ ΓΓΘΜ
Θ®2Θ©ΧΫΨΩ÷ΛΟςΘΚΑ―ΓςADE»ΤΒψAΡφ ±’κΖΫœρ–ΐΉΣΒΫΆΦ2ΒΡΈΜ÷ΟΘ§Ν§Ϋ”MNΘ§BDΘ§CEΘ§≈–ΕœΓςPMNΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©ΆΊ’Ι―”…λΘΚΑ―ΓςADE»ΤΒψA‘ΎΤΫΟφΡΎΉ‘”…–ΐΉΣΘ§»τADΘΫ4Θ§ABΘΫ10Θ§«κ÷±Ϋ”–¥≥ωΓςPMNΟφΜΐΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©PMΘΫPNΘ§PMΓΆPNΘΜΘ®2Θ©ΓςPMN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§÷ΛΟςœξΦϊΫβΈωΘΜΘ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο»ΐΫ«–ΈΒΡ÷–ΈΜœΏΒΟ≥ωPM=![]() CEΘ§PN=
CEΘ§PN=![]() BDΘ§ΫχΕχ≈–Εœ≥ωBD=CEΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ§‘Όάϊ”Ο»ΐΫ«–ΈΒΡ÷–ΈΜœΏΒΟ≥ωPMΓΈCEΒΟ≥ωΓœDPM=ΓœDCAΘ§ΉνΚσ”ΟΜΞ”ύΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
BDΘ§ΫχΕχ≈–Εœ≥ωBD=CEΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ§‘Όάϊ”Ο»ΐΫ«–ΈΒΡ÷–ΈΜœΏΒΟ≥ωPMΓΈCEΒΟ≥ωΓœDPM=ΓœDCAΘ§ΉνΚσ”ΟΜΞ”ύΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©œ»≈–Εœ≥ωΓςABDΓ’ΓςACEΘ§ΒΟ≥ωBD=CEΘ§Ά§Θ®1Θ©ΒΡΖΫΖ®ΒΟ≥ωPM=![]() BDΘ§PN=
BDΘ§PN=![]() BDΘ§Φ¥Ω…ΒΟ≥ωPM=PNΘ§Ά§Θ®1Θ©ΒΡΖΫΖ®Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
BDΘ§Φ¥Ω…ΒΟ≥ωPM=PNΘ§Ά§Θ®1Θ©ΒΡΖΫΖ®Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©ΖΫΖ®1ΓΔœ»≈–Εœ≥ωMNΉν¥σ ±Θ§ΓςPMNΒΡΟφΜΐΉν¥σΘ§ΫχΕχ«σ≥ωANΘ§AMΘ§Φ¥Ω…ΒΟ≥ωMNΉν¥σ=AM+ANΘ§ΉνΚσ”ΟΟφΜΐΙΪ ΫΦ¥Ω…ΒΟ≥ωΫα¬έΘ°
ΖΫΖ®2ΓΔœ»≈–Εœ≥ωBDΉν¥σ ±Θ§ΓςPMNΒΡΟφΜΐΉν¥σΘ§ΕχBDΉν¥σ «AB+AD=14Θ§Φ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΓΏΒψPΘ§N «BCΘ§CDΒΡ÷–ΒψΘ§
ΓύPNΓΈBDΘ§PNΘΫ![]() BDΘ§
BDȧ
ΓΏΒψPΘ§M «CDΘ§DEΒΡ÷–ΒψΘ§
ΓύPMΓΈCEΘ§PMΘΫ![]() CEΘ§
CEȧ
ΓΏABΘΫACΘ§ADΘΫAEΘ§
ΓύBDΘΫCEΘ§
ΓύPMΘΫPNΘ§
ÿPNøBDȧ
ΓύΓœDPNΘΫΓœADCΘ§
ÿPMøCEȧ
ΓύΓœDPMΘΫΓœDCAΘ§
ΓΏΓœBACΘΫ90ΓψΘ§
ΓύΓœADC+ΓœACDΘΫ90ΓψΘ§
ΓύΓœMPNΘΫΓœDPM+ΓœDPNΘΫΓœDCA+ΓœADCΘΫ90ΓψΘ§
ΓύPMΓΆPNΘ§
Ι ¥πΑΗΈΣΘΚPMΘΫPNΘ§PMΓΆPNΘΜ
Θ®2Θ©ΓςPMN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ°
”…–ΐΉΣ÷ΣΘ§ΓœBADΘΫΓœCAEΘ§
ΓΏABΘΫACΘ§ADΘΫAEΘ§
ΓύΓςABDΓ’ΓςACEΘ®SASΘ©Θ§
ΓύΓœABDΘΫΓœACEΘ§BDΘΫCEΘ§
άϊ”Ο»ΐΫ«–ΈΒΡ÷–ΈΜœΏΒΟΘ§PNΘΫ![]() BDΘ§PMΘΫ
BDΘ§PMΘΫ![]() CEΘ§
CEȧ
ΓύPMΘΫPNΘ§
ΓύΓςPMN «Β»―ϋ»ΐΫ«–ΈΘ§
Ά§Θ®1Θ©ΒΡΖΫΖ®ΒΟΘ§PMΓΈCEΘ§
ΓύΓœDPMΘΫΓœDCEΘ§
Ά§Θ®1Θ©ΒΡΖΫΖ®ΒΟΘ§PNΓΈBDΘ§
ΓύΓœPNCΘΫΓœDBCΘ§
ΓΏΓœDPNΘΫΓœDCB+ΓœPNCΘΫΓœDCB+ΓœDBCΘ§
ΓύΓœMPNΘΫΓœDPM+ΓœDPNΘΫΓœDCE+ΓœDCB+ΓœDBC
ΘΫΓœBCE+ΓœDBCΘΫΓœACB+ΓœACE+ΓœDBC
ΘΫΓœACB+ΓœABD+ΓœDBCΘΫΓœACB+ΓœABCΘ§
ΓΏΓœBACΘΫ90ΓψΘ§
ΓύΓœACB+ΓœABCΘΫ90ΓψΘ§
ΓύΓœMPNΘΫ90ΓψΘ§
ΓύΓςPMN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®3Θ©ΖΫΖ®1ΘΚ»γΆΦ2Θ§
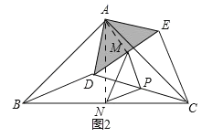
Ά§Θ®2Θ©ΒΡΖΫΖ®ΒΟΘ§ΓςPMN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύMNΉν¥σ ±Θ§ΓςPMNΒΡΟφΜΐΉν¥σΘ§
ΓύDEΓΈBC«“DE‘ΎΕΞΒψA…œΟφΘ§
ΓύMNΉν¥σΘΫAM+ANΘ§
ͧ۔AMȧANȧ
‘ΎΓςADE÷–Θ§ADΘΫAEΘΫ4Θ§ΓœDAEΘΫ90ΓψΘ§
ΓύAMΘΫ![]() Θ§
Θ§
‘ΎRtΓςABC÷–Θ§ABΘΫACΘΫ10Θ§ANΘΫ![]() Θ§
Θ§
ΓύMNΉν¥σΘΫ![]() Θ§
Θ§
ΓύSΓςPMNΉν¥σΘΫ![]() PM2ΘΫ
PM2ΘΫ![]() ΓΝ
ΓΝ![]() MN2ΘΫ
MN2ΘΫ![]() ΓΝΘ®
ΓΝΘ®![]() Θ©2ΘΫ
Θ©2ΘΫ![]() ΘΜ
ΘΜ
ΖΫΖ®2ΘΚ”…Θ®2Θ©÷ΣΘ§ΓςPMN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§PMΘΫPNΘΫ![]() BDΘ§
BDȧ
ΓύPMΉν¥σ ±Θ§ΓςPMNΟφΜΐΉν¥σΘ§
ΓύΒψD‘ΎBAΒΡ―”≥ΛœΏ…œΘ§
ΓύBDΘΫAB+ADΘΫ14Θ§
ΓύPMΘΫ7Θ§
ΓύSΓςPMNΉν¥σΘΫ![]() PM2ΘΫ
PM2ΘΫ![]() ΓΝ72ΘΫ
ΓΝ72ΘΫ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷–―ß…ζ…œ―ߥχ ÷ΜζΒΡœ÷œσ‘Ϋά¥‘Ϋ ήΒΫ…γΜαΒΡΙΊΉΔΘ§ΈΣ¥ΥΟΫΧεΦ«’ΏΥφΜζΒς≤ιΝΥΡ≥–Θ»τΗ…Οϊ―ß…ζ…œ―ߥχ ÷ΜζΒΡΡΩΒΡΘ§Ζ÷ΈΣΥΡ÷÷άύ–ΆΘΚAΫ”ΧΐΒγΜΑΘΜB ’ΖΔΕΧ–≈ΘΜC≤ι‘ΡΉ ΝœΘΜD”ΈœΖΝΡΧλΘ°≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…ΆΦ1ΚΆΆΦ2ΒΡΆ≥ΦΤΆΦΘ®≤ΜΆξ’ϊΘ©Θ§«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥Υ¥Έ≥ι―υΒς≤ι÷–Θ§Ι≤Βς≤ιΝΥΓΓ ΓΓΟϊ―ß…ζΘΜ
Θ®2Θ©ΫΪΆΦ1ΓΔΆΦ2≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©œ÷”–4Οϊ―ß…ζΘ§Τδ÷–AάύΝΫΟϊΘ§BάύΝΫΟϊΘ§¥”÷–»Έ―Γ2Οϊ―ß…ζΘ§«σ’βΝΫΟϊ―ß…ζΈΣΆ§“Μάύ–ΆΒΡΗ≈¬ Θ®”ΟΝ–±μΖ®Μρ ςΉ¥ΆΦΖ®Θ©Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫ––ΥΡ±Ώ–Έ![]() ÷–Θ§Ε‘Ϋ«œΏ
÷–Θ§Ε‘Ϋ«œΏ![]() ΓΔ
ΓΔ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Βψ
Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§―Ί
≥ωΖΔΘ§―Ί![]() ΖΫœρ‘»ΥΌ‘ΥΕ·Θ§ΥΌΕ»ΈΣ
ΖΫœρ‘»ΥΌ‘ΥΕ·Θ§ΥΌΕ»ΈΣ![]() ΘΜΆ§ ±Θ§Βψ
ΘΜΆ§ ±Θ§Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§―Ί
≥ωΖΔΘ§―Ί![]() ΖΫœρ‘»ΥΌ‘ΥΕ·Θ§ΥΌΕ»ΈΣ
ΖΫœρ‘»ΥΌ‘ΥΕ·Θ§ΥΌΕ»ΈΣ![]() ΘΜΒ±“ΜΗωΒψΆΘ÷Ι‘ΥΕ· ±Θ§Νμ“ΜΗωΒψ“≤ΆΘ÷Ι‘ΥΕ·Θ°Ν§Ϋ”
ΘΜΒ±“ΜΗωΒψΆΘ÷Ι‘ΥΕ· ±Θ§Νμ“ΜΗωΒψ“≤ΆΘ÷Ι‘ΥΕ·Θ°Ν§Ϋ”![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() Θ§…η‘ΥΕ· ±ΦδΈΣ
Θ§…η‘ΥΕ· ±ΦδΈΣ![]() Θ§
Θ§
Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Β±![]() ΈΣΚΈ÷Β ±
ΈΣΚΈ÷Β ±![]() «Β»―ϋ»ΐΫ«–ΈΘΩ
«Β»―ϋ»ΐΫ«–ΈΘΩ
Θ®2Θ©…ηΈε±Ώ–Έ![]() ΟφΜΐΈΣ
ΟφΜΐΈΣ![]() Θ§ ‘»ΖΕ®
Θ§ ‘»ΖΕ®![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ![]() Θ§ Ι
Θ§ Ι![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®4Θ©‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ![]() ΙΒΟ
ΙΒΟ![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§»τ¥φ‘ΎΘ§«σ≥ω
Θ§»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
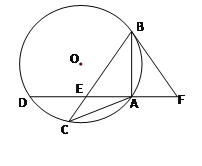
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΡΎΫ””ΎΓ―OΘ§«“ABΘΫACΘ§ΒψD‘ΎΓ―O…œΘ§ADΓΆAB”ΎΒψAΘ§ AD”κ BCΫΜ”ΎΒψEΘ§F‘ΎDAΒΡ―”≥ΛœΏ…œΘ§«“AFΘΫAEΘ°
(1)«σ÷ΛΘΚBF «Γ―OΒΡ«–œΏΘΜ
(2)»τADΘΫ4Θ§![]() Θ§«σBCΒΡ≥ΛΘ°
Θ§«σBCΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
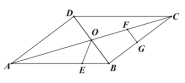
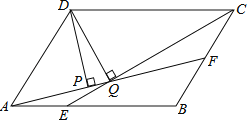
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§ABΘΫ3Θ§BCΘΫ2Θ§ΓœDABΘΫ60ΓψΘ§E‘ΎAB…œΘ§«“AEΘΫ![]() EBΘ§F «BCΒΡ÷–ΒψΘ§ΙΐDΖ÷±πΉςDPΓΆAF”ΎPΘ§DQΓΆCE”ΎQΘ§‘ρDPΘΚDQΒΡ÷ΒΈΣ_____Θ°
EBΘ§F «BCΒΡ÷–ΒψΘ§ΙΐDΖ÷±πΉςDPΓΆAF”ΎPΘ§DQΓΆCE”ΎQΘ§‘ρDPΘΚDQΒΡ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
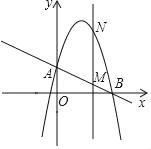
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=©¹x2+bx+cΘ®bΘ§c «≥Θ ΐΘ©Ψ≠ΙΐAΘ®0Θ§2Θ©ΓΔBΘ®4Θ§0Θ©ΝΫΒψΘ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΚΆΕΞΒψΉχ±ξΘΜ
Θ®2Θ©Ής¥Ι÷±x÷αΒΡ÷±œΏx=tΘ§‘ΎΒΎ“ΜœσœόΫΜ÷±œΏAB”ΎMΘ§ΫΜ’βΧθ≈ΉΈοœΏ”ΎNΘ§«σΒ±t»ΓΚΈ÷Β ±Θ§MN”–Ήν¥σ÷ΒΘΩΉν¥σ÷Β «Εύ…ΌΘΩ
Θ®3Θ©‘ΎΘ®1Θ©ΒΡ«ιΩωœ¬Θ§“‘AΓΔMΓΔNΓΔDΈΣΕΞΒψΉςΤΫ––ΥΡ±Ώ–ΈΘ§«κ÷±Ϋ”–¥≥ωΒΎΥΡΗωΕΞΒψDΒΡΥυ”–Ήχ±ξΘ®÷±Ϋ”–¥≥ωΫαΙϊΘ§≤Μ±Ί–¥Ϋβ¥πΙΐ≥ΧΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚλΤλΝ§Υχ≥§ –ΉΦ±ΗΙΚΫχΦΉΓΔ““ΝΫ÷÷¬Χ…Ϊ¥ϋΉΑ ≥ΤΖΘ°ΦΉΓΔ““ΝΫ÷÷¬Χ…Ϊ¥ϋΉΑ ≥ΤΖΒΡΫχΦέΚΆ έΦέ»γ±μΘ°“―÷ΣΘΚ”Ο2000‘ΣΙΚΫχΦΉ÷÷¥ϋΉΑ ≥ΤΖΒΡ ΐΝΩ”κ”Ο1600‘ΣΙΚΫχ““÷÷¥ϋΉΑ ≥ΤΖΒΡ ΐΝΩœύΆ§Θ°
ΦΉ | ““ | |
ΫχΦέΘ®‘Σ/¥ϋΘ© |
|
|
έΦέΘ®‘Σ/¥ϋΘ© | 20 | 13 |
Θ®1Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©“Σ ΙΙΚΫχΒΡΦΉΓΔ““ΝΫ÷÷¬Χ…Ϊ¥ϋΉΑ ≥ΤΖΙ≤800¥ϋΒΡΉήάϊ»σΘ®άϊ»σ= έΦέ-ΫχΦέΘ©≤Μ…Ό”Ύ4800‘ΣΘ§«“≤Μ≥§Ιΐ4900‘ΣΘ§Έ ΗΟ≥§ –”–ΦΗ÷÷ΫχΜθΖΫΑΗΘΩ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΗΟ≥§ –»γΙϊΕ‘ΦΉ÷÷¥ϋ―b ≥ΤΖΟΩ¥ϋ”≈Μί![]() ‘Σ≥ω έΘ§““÷÷¥ϋΉΑ ≥ΤΖΦέΗώ≤Μ±δΘ°Ρ«Ο¥ΗΟ≥§ –“ΣΜώΒΟΉν¥σάϊ»σ”Π»γΚΈΫχΜθΘΩ
‘Σ≥ω έΘ§““÷÷¥ϋΉΑ ≥ΤΖΦέΗώ≤Μ±δΘ°Ρ«Ο¥ΗΟ≥§ –“ΣΜώΒΟΉν¥σάϊ»σ”Π»γΚΈΫχΜθΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσΫΜ
ΒΡΆΦœσΫΜ![]() ÷α”Ύ
÷α”Ύ![]() ΝΫΒψΘ§ΫΜ
ΝΫΒψΘ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§ΕΞΒψ
Θ§ΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ°
Θ°

Θ®1Θ©«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΚΆ÷±œΏ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©Βψ![]() «÷±œΏ
«÷±œΏ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ
…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§Β±Βψ
Θ§Β±Βψ![]() ‘ΎΒΎ“Μœσœό ±Θ§«σœΏΕΈ
‘ΎΒΎ“Μœσœό ±Θ§«σœΏΕΈ![]() ≥ΛΕ»ΒΡΉν¥σ÷ΒΘΜ
≥ΛΕ»ΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“λ”Ύ![]() ΒΡΒψ
ΒΡΒψ![]() Θ§ Ι
Θ§ Ι![]() ÷–
÷–![]() ±Ώ…œΒΡΗΏΈΣ
±Ώ…œΒΡΗΏΈΣ![]() Θ§»τ¥φ‘Ύ«σ≥ωΒψ
Θ§»τ¥φ‘Ύ«σ≥ωΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘Ύ«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘Ύ«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
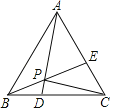
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§Β»±ΏΓςABCΒΡ±Ώ≥ΛΈΣ4Θ§ΒψD «BC±Ώ…œ“ΜΕ·ΒψΘ§«“CEΘΫBDΘ§Ν§Ϋ”ADΘ§BEΘ§AD”κBEœύΫΜ”ΎΒψPΘ§Ν§Ϋ”PCΘ°‘ρœΏΕΈPCΒΡΉν–Γ÷ΒΒ»”Ύ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com