
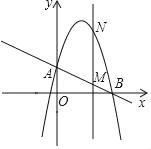
����Ŀ����ͼ����֪������y=��x2+bx+c��b��c�dz���������A��0��2����B��4��0�����㣮
��1����������ߵĽ���ʽ�Ͷ������ꣻ
��2������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB��M����������������N����tȡ��ֵʱ��MN�����ֵ�����ֵ�Ƕ��٣�
��3���ڣ�1��������£���A��M��N��DΪ������ƽ���ı��Σ���ֱ��д�����ĸ�����D���������ֱ꣨��д�����������д�����̣�
���𰸡���1�������߽���ʽΪy=��x2+![]() x+2�������ߵĶ�������Ϊ��
x+2�������ߵĶ�������Ϊ��![]() ��
��![]() ������2��t=2ʱ��MN�����ֵ�����ֵΪ4����3��D������Ϊ��0��6����0����2����4��4����
������2��t=2ʱ��MN�����ֵ�����ֵΪ4����3��D������Ϊ��0��6����0����2����4��4����
����������������1����A��B�����������������y=��x2+bx+c�ù���b��c����������ⷽ���鼴�ɵõ������߽���ʽ��Ȼ���һ��ʽ��ɶ���ʽ�õ������ߵĶ���������
��2�������ô���ϵ�������ֱ��AB�Ľ���ʽΪy=��![]() x+2����N��t����t2+
x+2����N��t����t2+![]() t+2����0��t��4������N��t����
t+2����0��t��4������N��t����![]() t+2������MN=��t2+
t+2������MN=��t2+![]() t+2������
t+2������![]() t+2����Ȼ�����ö��κ��������ʽ��������
t+2����Ȼ�����ö��κ��������ʽ��������
��3���ɣ�2����N��2��5����M��2��1������ͼ������ƽ���ı��ε����ʽ�����������MNΪƽ���ı��εı�ʱ������MN��AD��MN=AD=4��ȷ������D����������MNΪƽ���ı��εĶԽ���ʱ������AN��MN��AN=MD�͵�ƽ�Ƶ��������д����ӦD�����꣮
�������1����A��0��2����B��4��0������������y=��x2+bx+c��![]() �������
�������![]() ���������߽���ʽΪy=��x2+
���������߽���ʽΪy=��x2+![]() x+2��
x+2��
��y=��x2+![]() x+2=����x��
x+2=����x��![]() ��2+
��2+![]() ���������ߵĶ�������Ϊ��
���������ߵĶ�������Ϊ��![]() ����
����
��2����ֱ��AB�Ľ���ʽΪy=mx+n����A��0��2����B��4��0���������![]() �������
�������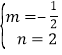 ����ֱ��AB�Ľ���ʽΪy=��
����ֱ��AB�Ľ���ʽΪy=��![]() x+2����N��t����t2+
x+2����N��t����t2+![]() t+2����0��t��4������N��t����
t+2����0��t��4������N��t����![]() t+2������MN=��t2+
t+2������MN=��t2+![]() t+2������
t+2������![]() t+2��=��t2+4t =����t��2��2+4��
t+2��=��t2+4t =����t��2��2+4��
��t=2ʱ��MN�����ֵ�����ֵΪ4��
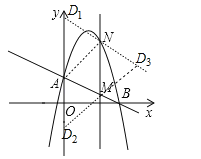
��3���ɣ�2����N��2��5����M��2��1������ͼ����MNΪƽ���ı��εı�ʱ��MN��AD��MN=AD=4����D1��0��6����D2��0����2������MNΪƽ���ı��εĶԽ���ʱ��AN��MN��AN=MD�����ڵ�A����ƽ��2����λ��������ƽ��3����λ�õ�N�������M����ƽ��2����λ��������ƽ��3����λ�õ�D������D3������Ϊ��4��4����
����������D��������0��6����0����2����4��4����


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�ͬʱ�����ס���������Ʒ��200��������ۺ��ۼ������
��Ʒ���� | �� | �� |
���ۣ�Ԫ/���� | 80 | 100 |
�ۼۣ�Ԫ/���� | 160 | 240 |
�����м�����Ʒ����x�������̳�������200����Ʒ��������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��
��2������Ʒ�ƻ����Ͷ��18000Ԫ���ڹ�����������Ʒ��������Ҫ�������ټ�����Ʒ����������Щ��Ʒ�����̳��ɻ�õ���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ֽ���ʽ����1��2x2+2xy��3x��3y����2��a2��b2+4a��4b
������̽������ij��ѧ��̽��ѧϰ��С���������ʽ�ֽ���Ŀ����������̽����
̽��1���ֽ���ʽ����1��2x2+2xy��3x��3y
�ö���ʽ����ֱ��ʹ����ȡ����ʽ������ʽ��������ʽ�ֽ⣮������ϸ�۲����ʽ���ص㣮���ָö���ʽǰ�����й���ʽ2x���������й���ʽ��3���ֱ�������������ʣ�µ�����ͬ��ʽ��x+y�������Լ������ṫ��ʽ���ֽ⣮
�⣺2x2+2xy��3x��3y����2x2+2xy������3x+3y����2x��x+y����3��x+y������x+y����2x��3��
�����ҷ��ָö���ʽ�ĵڶ���͵�����й���ʽy����һ��͵�����й���ʽx����y��x�������ʣ�µ�����ͬ��ʽ��2x��3�������Լ������ṫ��ʽ���ֽ⣮
�⣺2x2+2xy��3x��3y����2x2��3x��+��2xy��3y����x��2x��3��+y��2x��3������2x��3����x+y��
̽��2���ֽ���ʽ����2��a2��b2+4a��4b
�ö���ʽ���ֱ��ʹ����ȡ����ʽ������ʽ��������ʽ�ֽ⣬�����������ⰴ̽��1�ķ������飬������a�������һ�鼴a2+4a��a��a+4��������b����һ�鼴��b2��4b����b��b+4����������a��a+4���멁b��b+4����û�й���ʽ���ᣬ���ٷֽ���ȥ����������ϸ�۲췢�֣����Ƚ�a2��b2����һ��Ӧ��ƽ���ʽ�����������һ�飬�������ʽ4����ɼ����������ʽ���Ӷ��ﵽ�ֽ���ʽ��Ŀ�ģ�
�⣺a2��b2+4a��4b����a2��b2��+��4a��4b������a+b����a��b��+4��a��b������a��b����4+a+b��
�������ܽᣩ���Բ���ֱ��ʹ����ȡ����ʽ������ʽ�����зֽ���ʽ�Ķ���ʽ�����ǿɿ��ǰѱ��ֽ�Ķ���ʽ�ֳ������飬�ֱ𰴡���������������ȡ����ʽ�������ù�ʽ�����зֽ⣬Ȼ���ۺ��������ٴ������ϰ��������������������зֽ⣬ֱ���ֽ������������ַֽ���ʽ�ķ�����������ֽⷨ��
����ֽⷨ������һ�ֶ�������ʽ�ֽ�ķ���������ͨ���Զ���ʽ�����ʵ��ķ��飬�Ѷ���ʽת��Ϊ����Ӧ�á������������ֽ�Ľṹ��ʽ��ʹ֮���й���ʽ�����߷��Ϲ�ʽ���ص�ȣ��Ӷ��ﵽ�������á��������������зֽ���ʽ��Ŀ�ģ�
��ѧ�����ã����������÷���ֽⷨ����������⣺
��1���ֽ���ʽ��![]()
��2���ֽ���ʽ��![]()
����չ��������
��3��������������˼·�ֽ���ʽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
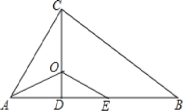
����Ŀ����ͼ����ABC�У���ACB=90����CD��AB�ڵ�D��AOƽ�֡�BAC����CD�ڵ�O��EΪAB��һ�㣬��AE=AC��
��1����֤����AOC�ա�AOE��
��2����֤��OE��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
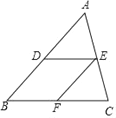
����Ŀ����ͼ���ڡ�ABC�У�D��AB�е㣬E��AC�е㣬F��BC�е㣬����գ�
��1���ı���BDEF���� ���ı��Σ�
��2�����ı���BDEF�����Σ����ABC������������� ����
��3�����ı���BDEF�Ǿ��Σ����ABC������������� ����
��4�����ı���BDEF�������Σ����ABC������������� ����
���ͣ�2������3������4����ѡȡһ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����8����ͬ��С�����ε�שƴ��һ����ε�ש.

��1��ÿ��С�����ε�ש�ij��Ϳ��ֱ��Ƕ��٣���Ҫ���з�������н��
��2��С������һ�����Ϊ![]() �������ε�̺�����űߵķ���ü���һ���µij����ε�̺��������ס�����ε�ש���С����һ�㣬���ܼ�������Ҫ��ĵ�̺��
�������ε�̺�����űߵķ���ü���һ���µij����ε�̺��������ס�����ε�ש���С����һ�㣬���ܼ�������Ҫ��ĵ�̺��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
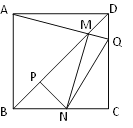
����Ŀ����ͼ���߳�һ����������ABCD��Q��CD��һ���㣬AQ��BD�ڵ�M����M��MN��AQ��BC��N�㣬��NP��BD�ڵ�P������NQ�����н��ۣ���AM=MN��
��MP=![]() BD����BN+DQ=NQ����
BD����BN+DQ=NQ����![]() Ϊ��ֵ������һ����������_______.
Ϊ��ֵ������һ����������_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
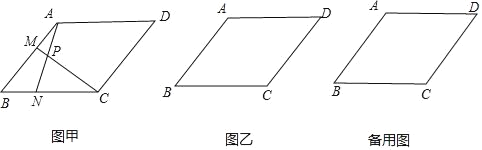
����Ŀ����ABCD�У�AB��BC��9����BCD��120�㣮��M�ӵ�A����������AB�����ƶ���ͬʱ��N�ӵ�B����������ͬ���ٶ�������BC�����ƶ�������AN��CM��ֱ��AN��CM�ཻ�ڵ�P��
��1����ͼ�ף�����M��N�ֱ��ڱ�AB��BC��ʱ��
����֤��AN��CM��
������MN������BMN��ֱ��������ʱ����AM��ֵ��
��2����M��N�ֱ��ڱ�AB��BC���ӳ�����ʱ����ͼ���л�����P����ֱ��д����CPN�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
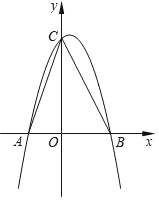
����Ŀ��������y=ax2+bx+3��a��0��������A����1��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE���AOC����ʱ�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com