
【题目】在ABCD中,AB=BC=9,∠BCD=120°.点M从点A出发沿射线AB方向移动.同时点N从点B出发,以相同的速度沿射线BC方向移动,连接AN,CM,直线AN、CM相交于点P.
(1)如图甲,当点M、N分别在边AB、BC上时,
①求证:AN=CM;
②连接MN,当△BMN是直角三角形时,求AM的值.
(2)当M、N分别在边AB、BC的延长线上时,在图乙中画出点P,并直接写出∠CPN的度数.
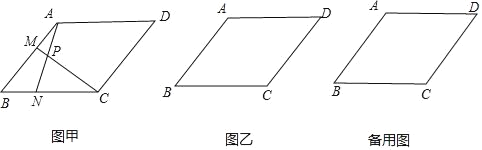
【答案】(1)①见解析②3或6(2)120°
【解析】
(1)①连接AC,先证△ABC是等边三角形得AB=CA=9、∠B=∠CAB=60°,由BN=AM证△ABN≌△CAM即可得;
②分∠MNB=90°和∠NMB=90°两种情况,由∠B=60°得出另一个锐角为30°,根据直角三角形中30°角所对边等于斜边的一半及AM=BN求解可得;
(2)根据题意作出图形,连接AC,先证△BAN≌△ACM得∠N=∠M,由∠NCP=∠MCB知∠CPN=∠CBM,根据AB∥CD、∠BCD=120°可得∠CPN=∠CBM=120°.
(1)①如图1,连接AC,
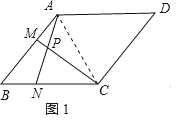
在ABCD中,AB∥DC,
∴∠B=180°﹣∠BCD=180°﹣120°=60°,
又∵AB=BC=9,
∴△ABC是等边三角形,
∴AB=CA=9,∠B=∠CAB=60°,
又∵BN=AM,
∴△ABN≌△CAM(SAS),
∴AN=CM;
②如图2,
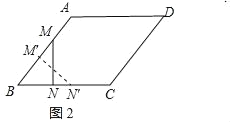
(Ⅰ)当∠MNB=90°时,
∵∠B=60°,
∴∠BMN=90°﹣60°=30°,
∴BN=![]() BM,
BM,
又∵BN=AM,
∴AM=![]() (9﹣AM),
(9﹣AM),
∴AM=3;
(Ⅱ)当∠NMB=90°时,∠BNM=90°﹣60°=30°,
∴BM=![]() BN,
BN,
∴9﹣AM=![]() AM,
AM,
∴AM=6;
综上所述,当△BMN是直角三角形时,AM的值为3或6;
(2)如图3所示,
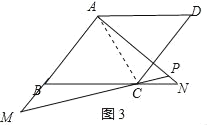
点P即为所求;
∠CPN=120°,
连接AC,
由(1)知△ABC是等边三角形,
∴∠BAN=∠CAM=60°、AB=CA,
又∵BN=AM,
∴△BAN≌△ACM(SAS),
∴∠N=∠M,
∵∠NCP=∠MCB,
∴∠CPN=∠CBM,
∵AB∥CD,∠BCD=120°,
∴∠CPN=∠CBM=120°.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
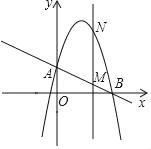
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
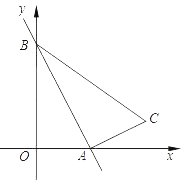
【题目】已知一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC=90°,tan∠ABC=![]() .
.
(1)求点C的坐标;
(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得2S△ABM=S△ABC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
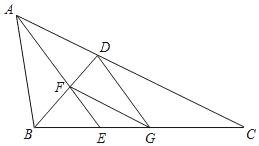
【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
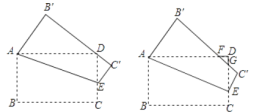
【题目】如图,在矩形纸片ABCD中,已知AB=2,BC=![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
(1)当点E与点C重合时,求DF的长
(2)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C’M的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4, ![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。

(1)、根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)、求一次函数解析式及m的值;
(3)、P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com