
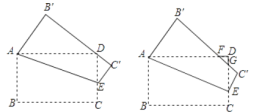
【题目】如图,在矩形纸片ABCD中,已知AB=2,BC=![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折得到多边形AB’C’E,点B、C的对应点分别为点B’,C’
(1)当点E与点C重合时,求DF的长
(2)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C’M的最小值
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】(问题提出):分解因式:(1)2x2+2xy﹣3x﹣3y;(2)a2﹣b2+4a﹣4b
(问题探究):某数学“探究学习”小组对以上因式分解题目进行了如下探究:
探究1:分解因式:(1)2x2+2xy﹣3x﹣3y
该多项式不能直接使用提取公因式法,公式法进行因式分解.于是仔细观察多项式的特点.甲发现该多项式前两项有公因式2x,后两项有公因式﹣3,分别把它们提出来,剩下的是相同因式(x+y),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2+2xy)﹣(3x+3y)=2x(x+y)﹣3(x+y)=(x+y)(2x﹣3)
另:乙发现该多项式的第二项和第四项含有公因式y,第一项和第三项含有公因式x,把y、x提出来,剩下的是相同因式(2x﹣3),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2﹣3x)+(2xy﹣3y)=x(2x﹣3)+y(2x﹣3)=(2x﹣3)(x+y)
探究2:分解因式:(2)a2﹣b2+4a﹣4b
该多项式亦不能直接使用提取公因式法,公式法进行因式分解,于是若将此题按探究1的方法分组,将含有a的项分在一组即a2+4a=a(a+4),含有b的项一组即﹣b2﹣4b=﹣b(b+4),但发现a(a+4)与﹣b(b+4)再没有公因式可提,无法再分解下去.于是再仔细观察发现,若先将a2﹣b2看作一组应用平方差公式,其余两项看作一组,提出公因式4,则可继续再提出因式,从而达到分解因式的目的.
解:a2﹣b2+4a﹣4b=(a2﹣b2)+(4a﹣4b)=(a+b)(a﹣b)+4(a﹣b)=(a﹣b)(4+a+b)
(方法总结):对不能直接使用提取公因式法,公式法进行分解因式的多项式,我们可考虑把被分解的多项式分成若干组,分别按“基本方法”即提取公因式法和运用公式法进行分解,然后,综合起来,再从总体上按“基本方法”继续进行分解,直到分解出最后结果.这种分解因式的方法叫做分组分解法.
分组分解法并不是一种独立的因式分解的方法,而是通过对多项式进行适当的分组,把多项式转化为可以应用“基本方法”分解的结构形式,使之具有公因式,或者符合公式的特点等,从而达到可以利用“基本方法”进行分解因式的目的.
(学以致用):尝试运用分组分解法解答下列问题:
(1)分解因式:![]()
(2)分解因式:![]()
(拓展提升):
(3)尝试运用以上思路分解因式:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
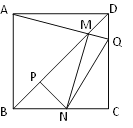
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
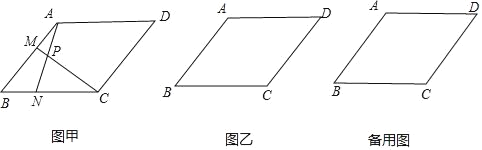
【题目】在ABCD中,AB=BC=9,∠BCD=120°.点M从点A出发沿射线AB方向移动.同时点N从点B出发,以相同的速度沿射线BC方向移动,连接AN,CM,直线AN、CM相交于点P.
(1)如图甲,当点M、N分别在边AB、BC上时,
①求证:AN=CM;
②连接MN,当△BMN是直角三角形时,求AM的值.
(2)当M、N分别在边AB、BC的延长线上时,在图乙中画出点P,并直接写出∠CPN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“![]() ”或“
”或“![]() ”填空:
”填空:
(1)如果![]() ,
,![]() ,那么a________b;
,那么a________b;
(2)如果![]() ,
,![]() ,那么a____b;
,那么a____b;
(3)如果![]() ,
,![]() ,那么a____b;
,那么a____b;
(4)当![]() ,b____0时,或者
,b____0时,或者![]() ,b___0时,有
,b___0时,有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
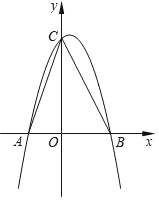
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
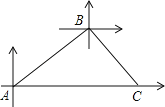
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com