
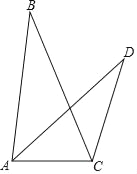
【题目】如图,在△ABC和△ACD中,∠B=∠D,tanB=![]() ,BC=5,CD=3,∠BCA=90°﹣
,BC=5,CD=3,∠BCA=90°﹣![]() ∠BCD,则AD=_____.
∠BCD,则AD=_____.
【答案】![]()
【解析】解:在BC上取一点F,使BF=CD=3,连接AF,
∴CF=BC﹣BF=5﹣3=2,
过F作FG⊥AB于G,
∵tanB=![]() =
=![]() ,
,
设FG=x,BG=2x,则BF=![]() x,
x,
∴![]() x=3,
x=3,
x=![]() ,
,
即FG=![]() ,
,
延长AC至E,连接BD,
∵∠BCA=90°﹣![]() ∠BCD,
∠BCD,
∴2∠BCA+∠BCD=180°,
∵∠BCA+∠BCD+∠DCE=180°,
∴∠BCA=∠DCE,
∵∠ABC=∠ADC,
∴A、B、D、C四点共圆,
∴∠DCE=∠ABD,∠BCA=∠ADB,
∴∠ABD=∠ADB,
∴AB=AD,
在△ABF和△ADC中,
∵ ,
,
∴△ABF≌△ADC(SAS),
∴AF=AC,
过A作AH⊥BC于H,
∴FH=HC=![]() FC=1,
FC=1,
由勾股定理得:AB2=BH2+AH2=42+AH2①,
S△ABF=![]() ABGF=
ABGF=![]() BFAH,
BFAH,
∴AB![]() =3AH,
=3AH,
∴AH=![]() ,
,
∴AH2=![]() ②,
②,
把②代入①得:AB2=16+![]() ,
,
解得:AB=![]() ,
,
∵AB>0,
∴AD=AB=2![]() ,
,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】沙坪坝区2017年已经成功创建国家卫生城区,现在正全力争创全国文明城区(简称“创文”),某街道积极响应“创文”活动,投入一定资金用于绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好,该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了![]() ,乙种树木单价下降了
,乙种树木单价下降了![]() ,且总费用不超过6804元,求
,且总费用不超过6804元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC,其中正确结论的序号是______.
EC,其中正确结论的序号是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠AOD交CD于E,OF⊥EO,OG⊥CD,∠D=50°,则下列结论:①∠AOE=60°;②∠DOF=25°;③∠GOE=∠DOF;④OF平分∠BOD,其中正确的个数是( )
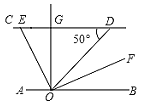
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2550元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于A,B两点,且点B坐标为(3,0).
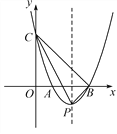
(1)求抛物线的表达式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
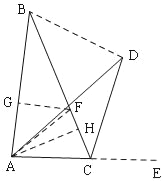
【题目】点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.
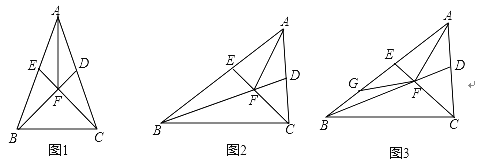
(1)如图1,若∠AEF=∠ADF,求证:AE=AD;
(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;
(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com