
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于A,B两点,且点B坐标为(3,0).
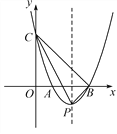
(1)求抛物线的表达式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
【答案】(1)抛物线的表达式为y=x2-4x+3;(2)△CPB的面积为3
【解析】试题分析: (1)将已知点的坐标代入二次函数的解析式,解关于![]() 的二元一次方程组即可;
的二元一次方程组即可;
(2)过点P作PH⊥Y轴于点H,过点B作BM∥y轴交直线PH于点M,过点C作CN⊥y轴叫直线BM于点N,则S△CPB=S矩形CHMNS△CHPS△PMBS△CNB由此计算即可;
试题解析: (1)∵抛物线![]() 经过点(1,8)与点B(3,0),
经过点(1,8)与点B(3,0),
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]()
(2)![]()
∴P(2,1)
过点P作PH⊥Y轴于点H,过点B作BM∥y轴交直线PH于点M,过点C作CN⊥y轴叫直线BM于点N,如下图所示:

S△CPB=S矩形CHMNS△CHPS△PMBS△CNB![]()
即:△CPB的面积为3.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AE=6,求AF的长.
,AE=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
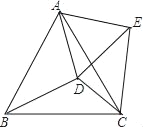
【题目】如图,在等边△ABC 内有一点D,AD=5,BD=6,CD=4,将线段AD绕点A旋转到AE,使∠DAE=∠BAC,连接EC.
(1)求CE的长;
(2)求cos∠CDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,顶点B的坐标为(n,2),点E是AB的中点,在OA上取一点D,将△BAD沿BD翻折,点A刚好落在BC边上的F处,BD、EF交于点P
(1)直接写出点E、F的坐标;
(2)若OD=1,求P点的坐标;
(3)动点Q从P点出发,依次经过F,y轴上的点M,x轴上的点N,然后返回到P点:
①若要使Q点运动一周的路径最短,试确定M、N的位置;
②若n=3,求最短路径的四边形PFMN的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣4,0)、B(0,﹣4)、C(2,0)三点,若点M为第三象限内抛物线上一动点,△AMB的面积为S,则S的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com