
【题目】如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为_________.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠AOD交CD于E,OF⊥EO,OG⊥CD,∠D=50°,则下列结论:①∠AOE=60°;②∠DOF=25°;③∠GOE=∠DOF;④OF平分∠BOD,其中正确的个数是( )
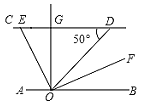
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△CDE是以C为公共顶点的两个三角形.
(1)如图1,当△ABC和△CDE都是等边三角形时,连接BD、AE相交于点P.求∠DPE的度数;
(2)如图2,当△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°时,连接AD、BE,Q为AD中点,连接QC并延长交BE于K.求证:QK⊥BE;
(3)在(1)的条件下,N是线段AE与CD的交点,PF是∠DPE的平分线,与DC交于点F,CN=2![]() ,∠PFN=45°,求FN的长.
,∠PFN=45°,求FN的长.
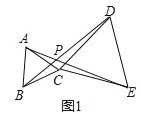
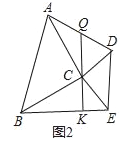
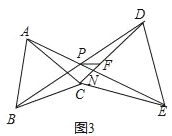
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于A,B两点,且点B坐标为(3,0).
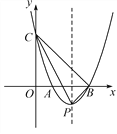
(1)求抛物线的表达式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角坐标系中直线 AB 与 x 轴正半轴、y 轴正半轴交于 A,B 两点,已知 B(0,4),∠BAO=30°,P,Q 分别是线段 OB,AB 上的两个动点,P 从 O 出发以每秒 3 个单位长度的速度向终点 B 运动,Q 从 B 出发以每秒 8 个单位长度的速度向终点 A 运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为 t(秒).
(1)求线段 AB 的长,及点 A 的坐标;
(2)t 为何值时,△BPQ 的面积为![]() ;
;
(3)若 C 为 OA 的中点,连接 QC,QP,以 QC,QP 为邻边作平行四边形 PQCD,
①t 为何值时,点 D 恰好落在坐标轴上;
②是否存在时间 t 使 x 轴恰好将平行四边形 PQCD 的面积分成 1∶3 的两部分,若存在,直接写出 t 的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠BAC=450,AD⊥BC于点D,BD=2,DC=3,求AD的长。某同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照这位同学的思路,探究并解答下列问题:
(1)分别以AB,AC为对称轴,作出△ABD,△ACD的轴对称图形,点D的对称点分别为E,F,延长EB,FC交于点G,证明四边形AEGF是正方形;
(2)设AD=x,建立关于x的方程模型,求出AD的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com