
����Ŀ����ͼ,����ABC��,��֪��BAC=450��AD��BC�ڵ�D��BD=2��DC=3����AD�ij���ijͬѧ���������Գ�֪ʶ����ͼ�ν��з��۱任������ؽ���˴��⡣�밴����λͬѧ��˼·��̽��������������⣺
��1���ֱ���AB��ACΪ�Գ��ᣬ������ABD����ACD����Գ�ͼ�Σ���D�ĶԳƵ�ֱ�ΪE��F���ӳ�EB��FC���ڵ�G��֤���ı���AEGF�������Σ�
��2����AD=x����������x�ķ���ģ�ͣ����AD��ֵ��

���𰸡���1������������2��AD=6.
��������
��1���ȸ�����ABD�ա�ABE����ACD�ա�ACF���ó���EAF=90�����ٸ��ݡ�E=��ADB=90��,��F=��ADC=90���ж��ı���AEGF�Ǿ��Σ� �����AE=AF�Ӷ�˵������AEGF�������Σ�
��2�����ù��ɶ�������������x�ķ��̣�x-2��2+��x-3��2=52�����AD=x=6��
(1)֤����������ɵã���ABD�ա�ABE,��ACD�ա�ACF.
���DAB=��EAB,��DAC=��FAC,�֡�BAC=45����
���EAF=90��.
�֡�AD��BC��
���E=��ADB=90��,��F=��ADC=90��.
���ı���AEGF�Ǿ��Σ�
�֡�AE=AD��AF=AD
��AE=AF.
�����AEGF��������.
(2)��AD=x����AE=EG=GF=x.
��BD=2��DC=3
��BE=2��CF=3
��BG=x2��CG=x3
��Rt��BGC��,BG2+CG2=BC2��
��(x2)2+(x3)2=52.
�����,x25x6=0
���x1=6,x2=1(��ȥ)
����AD=x=6.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=6cm����A=60������E��1cm/s���ٶ���AB����A��B�����˶���ͬʱ��F��2cm/s���ٶ���CB����C��B�˶���F�����Bʱ����ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬����DEFΪ�ȱ�������ʱ��t��ֵΪ_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�ڣ���֪��P��3��3����A��0��b����y����һ�㣬��P��PA�Ĵ��߽�x����B��a��0�������Q��a��b��Ϊ��P��һ�������㡣
��1��д����P�IJ�ͬ������������������� �� ��
��2������P�Ĺ�����Q��x��y������5x-3y=14�����Q�����ꣻ

��3����֪C��-1��-1��������A����B������������������������˶�������CAB��������ֵ����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�����C��CE��BC���Խ���BD�ڵ�E����DE=CE����![]() ����DE=_____.
����DE=_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�EΪCD��һ�㣬FΪBC���ӳ�����һ�㣬��CE=CF.BE��DF֮���������Ĺ�ϵ����˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����߾���A����4��0����B��0����4����C��2��0������������MΪ������������������һ��������AMB�����ΪS����S�����ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����BD����BD��CD������A��AM��BD�ڵ�M������D��DN��AB�ڵ�N����DN��![]() ����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.
����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α���չ
��֪���⣺
��������֤���������ε�һ����ǵ������������ڵ������ڽǵĺͣ���ô�������ε�һ���ڽ����������ڵ�������ǵĺ�֮�����������������ϵ�أ�
����̽��

��1����ͼ1����DBC���ECB�ֱ�Ϊ��ABC��������ǣ���̽����A���DBC+��ECB֮�����������������ϵ��Ϊʲô��
����Ӧ�ã�
��2����ͼ2���ڡ�ABCֽƬ�м�ȥ��CED���õ��ı���ABDE����1=130�㣬���2-��C=______��
��3��С�����뵽�����������һ�����⣺��ͼ3���ڡ�ABC�У�BP��CP�ֱ�ƽ����ǡ�DBC����ECB����P���A�к�������ϵ������������Ľ���ֱ��д����______��
3��չ������
��4����ͼ4�����ı���ABCD�У�BP��CP�ֱ�ƽ����ǡ�EBC����FCB����P���A����D�к�������ϵ��Ϊʲô��������Ҫ��������Ľ���˵������ֱ��ʹ�ã�����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
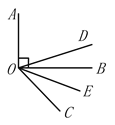
����Ŀ����ͼ��DOƽ����AOC��OEƽ����BOC����OA��OB��
��1������BOC��30�㣬��DOE��_______________�� ����BOC��60�㣬��DOE��_______________��
��2��ͨ������ļ��㣬�����DOE�Ķ������AOB��ʲô��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com