
����Ŀ����ͼ����֪A(��4�� ![]() )��B��-1,2����һ�κ���y=kx+b�뷴��������y=
)��B��-1,2����һ�κ���y=kx+b�뷴��������y=![]() (m��0��m��0)ͼ����������㣬AC��x����C��BD��y����D��
(m��0��m��0)ͼ����������㣬AC��x����C��BD��y����D��

(1)������ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��һ�κ������ڷ�����������ֵ?
(2)����һ�κ�������ʽ��m��ֵ��
(3)��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA����PDB�����ȣ����P���ꡣ
���𰸡�(1)����4��x����1��(2)��y=![]() ��m=��2��(3)����
��m=��2��(3)����![]() ��
��![]() ��
��
�����������������(1)������ͼʾֱ�ӵó��𰸣�(2)����A��B�����������һ�κ�������ʽ���k��b��ֵ������B��������뷴������������ʽ���m��ֵ��(3)�����ȸ���һ�κ��������P�����꣬���AC��OC��BD��OD�ij��ȣ�������PCA����PDB���������г�����x�ķ������x��ֵ��Ȼ��ó���P������.
���������(1)����ͼ����4��x����1ʱ��һ�κ���ֵ���ڷ�����������ֵ��
(2)����A(��4�� ![]() )��B����1��2������y=kx+b�ã�
)��B����1��2������y=kx+b�ã� 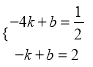 ��ã�
��ã� 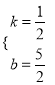
�� һ�κ����Ľ���ʽΪy=![]()
��B����1��2������y=![]() ��m=��2����m��ֵΪ��2��
��m=��2����m��ֵΪ��2��
(3)����P������Ϊ��x�� ![]() ������A��B�������֪AC=
������A��B�������֪AC=![]() ��OC=4��BD=1��OD=2��
��OC=4��BD=1��OD=2��
��֪��PCA�ĸ�Ϊx+4����PDB�ĸ�2��(![]() )����
)����![]() �ɵ�
�ɵ�
![]() �����
�����![]() ����ʱ
����ʱ![]()
�� P��������![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y=2x�ͺ���y=![]() ��ͼ����A��B���㣬����A��AE��x���ڵ�E������AOE�����Ϊ4��P������ƽ���ϵĵ㣬���Ե�B��O��E��PΪ������ı�����ƽ���ı��Σ���k= ������������P�������� ��
��ͼ����A��B���㣬����A��AE��x���ڵ�E������AOE�����Ϊ4��P������ƽ���ϵĵ㣬���Ե�B��O��E��PΪ������ı�����ƽ���ı��Σ���k= ������������P�������� ��
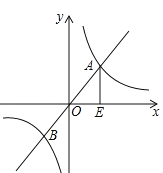
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������к�������y��![]() ����y��
����y��![]() x��1����y����3x��1����y��
x��1����y����3x��1����y��![]() ����y����
����y����![]() (x>0)����y��
(x>0)����y��![]() (x<0)������y��x�������������______(�����)��
(x<0)������y��x�������������______(�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8������ͼ����ƽ��ֱ������ϵ��������ABCD�Ķ���C��ԭ��O�غ�����B��y���������������A�ں���y=![]() ��k>0��x>0����ͼ��������D������Ϊ��4��3����
��k>0��x>0����ͼ��������D������Ϊ��4��3����
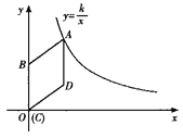
��1����k��ֵ��
��2����������ABCD��x��������ƽ���������εĶ���D���ں���y=![]() ��k>0��x>0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ�����
��k>0��x>0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ͼ��ʾ������ͼ��ɵã� 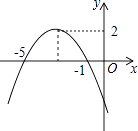
��1�������߶���������
��2���Գ���Ϊ
��3����x=ʱ��y�����ֵ����
��4����ʱ��y����x�����������
��5����ʱ��y��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��b��ͼ���뷴��������y��![]() ��ͼ���ڵ�һ�����ڵ�A(4��2)����y��ĸ����ύ�ڵ�B����OB��6.
��ͼ���ڵ�һ�����ڵ�A(4��2)����y��ĸ����ύ�ڵ�B����OB��6.
(1)����y��![]() ��y��kx��b�Ľ���ʽ��
��y��kx��b�Ľ���ʽ��
(2)��ֱ֪��AB��x���ཻ�ڵ�C���ڵ�һ�����ڣ���������y��![]() ��ͼ����һ��P��ʹ��S��POC��9.
��ͼ����һ��P��ʹ��S��POC��9.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������1��3��5��7��9�������ų���ͼ7��ʾ������
��1��ʮ�ֿ��е�������ĺ����м���15��ʲô��ϵ��
��2�����м���Ϊ![]() ����ʽ�ӱ�ʾʮ�ֿ��������֮�ͣ�
����ʽ�ӱ�ʾʮ�ֿ��������֮�ͣ�
��3������ʮ�ֿ������������ƶ����ɿ�ס�������������������ĺͻ������ֹ�����
��4��ʮ�ֿ��������֮���ܵ���2005�����ܣ���д����������������ܣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣���ͼ���ı���ABCD�У�![]() ,E�DZ�CD���е㣬����BE���ӳ���AD���ӳ�������ڵ�F��
,E�DZ�CD���е㣬����BE���ӳ���AD���ӳ�������ڵ�F��

��1����֤���ı���BDFC��ƽ���ı��Σ�
��2������BCD�ǵ��������Σ����ı���BDFC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�
��1��x2��2x��8=0��
��2��3x��x��1��=2��x��1����
��3��x2+3=3��x+1����
��4��2x��4x+5��=7��
��5��4x2��8x+1=0��
��6����y+2��2=��3y��1��2 ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com