
【题目】已知函数图象如图所示,根据图象可得: 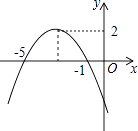
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
【答案】
(1)(﹣3,2)
(2)x=﹣3
(3)-3;2
(4)x<﹣3
(5)﹣5<x<﹣1
【解析】解:(1)∵抛物线与x轴交于点(﹣5,0),(﹣1,0),
∴顶点横坐标为 ![]() =﹣3,
=﹣3,
由图可知顶点纵坐标为2,
∴顶点坐标为(﹣3,2);(2)对称轴为x=﹣3;(3)当x=﹣3时,y有最大值是2;(4)当x<﹣3时,y随着x得增大而增大;(5)当﹣5<x<﹣1时,y>0.
所以答案是(1)(﹣3,2);(2)x=﹣3;(3)﹣3,2;(4)x<﹣3;(5)﹣5<x<﹣1.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字. 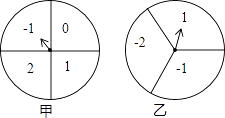
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=![]() (k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为
(k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为![]() ,点C的横坐标为1.
,点C的横坐标为1.
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4, ![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。

(1)、根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)、求一次函数解析式及m的值;
(3)、P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,数学家高斯在上学时曾经研究过这样一个问题,1+2+3+…+10=?经过研究,这个问题的一般性结论是1+2+3+…+n=![]() n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
观察下面三个特殊的等式:
1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
读完这段材料,请你计算:
(1)1×2+2×3+…+100×101;
(2)1×2+2×3+…+ n(n+1);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?( ![]() =1.414)
=1.414) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com