
【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=![]() (k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为
(k2>0)在第一象限的图象交于C,D两点,点O为坐标原点,△AOB的面积为![]() ,点C的横坐标为1.
,点C的横坐标为1.
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.

【答案】(1) y=-x+7. y=![]() .(2) (2,4),(3,3),(4,2).
.(2) (2,4),(3,3),(4,2).
【解析】(1)分别令x=0、y=0,求得对应y和x的值,从而的得到点A、B的坐标,然后依据三角形的面积公式可求得k1的值,然后由直线的解析式可求得点C的坐标,由点C的坐标可求得反比例函数的解析式;
(2)由函数的对称性可求得D(6,1),从而可求得x的值范围,然后求得当x=2、3、4、5时,一次函数和反比例函数对应的函数值,从而可得到整点的坐标.
(1)∵当x=0时,y=7,当y=0时,x=-![]() ,
,
∴A(-![]() ,0)、B(0、7).
,0)、B(0、7).
∴S△AOB=![]() |OA||OB|=
|OA||OB|=![]() ×(-
×(-![]() )×7=
)×7=![]() ,解得k1=-1.
,解得k1=-1.
∴直线的解析式为y=-x+7.
∵当x=1时,y=-1+7=6,
∴C(1,6).
∴k2=1×6=6.
∴反比例函数的解析式为y=![]() .
.
(2)∵点C与点D关于y=x对称,
∴D(6,1).
当x=2时,反比例函数图象上的点为(2,3),直线上的点为(2,5),此时可得整点为(2,4);
当x=3时,反比例函数图象上的点为(3,2),直线上的点为(3,4),此时可得整点为(3,3);
当x=4时,反比例函数图象上的点为(4,![]() ),直线上的点为(4,3),此时可得整点为(4,2);
),直线上的点为(4,3),此时可得整点为(4,2);
当x=5时,反比例函数图象上的点为(5,![]() ),直线上的点为(5,2),此时,不存在整点.
),直线上的点为(5,2),此时,不存在整点.
综上所述,符合条件的整点有(2,4)、(3,3)、(4,2).


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°. 
(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= ![]() AE;
AE;
(2)当α=90°时(如图2),求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).

(1)当t为何值时,四边形PQDC是平行四边形
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列函数:①y=![]() ;②y=
;②y=![]() x-1;③y=-3x+1;④y=
x-1;③y=-3x+1;④y=![]() ;⑤y=-
;⑤y=-![]() (x>0);⑥y=
(x>0);⑥y=![]() (x<0).其中y随x的增大而减小的是______(填序号).
(x<0).其中y随x的增大而减小的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数的序号填到相应的横线上:
①+5,②-3,③0,④-1.414,⑤17,⑥-![]() .
.
正整数:______________________________________________________;
负分数:______________________________________________________;
负有理数:____________________________________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
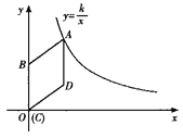
【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数图象如图所示,根据图象可得: 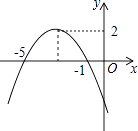
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,排成如图7所示的数阵.
(1)十字框中的五个数的和与中间数15有什么关系?
(2)设中间数为![]() ,用式子表示十字框中五个数之和;
,用式子表示十字框中五个数之和;
(3)若将十字框中上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?
(4)十字框中五个数之和能等于2005吗?若能,请写出这五个数;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com