
【题目】某商场同时购进甲、乙两种商品共200件,其进价和售价如表,
商品名称 | 甲 | 乙 |
进价(元/件) | 80 | 100 |
售价(元/件) | 160 | 240 |
设其中甲种商品购进x件,该商场售完这200件商品的总利润为y元.
(1)求y与x的函数关系式;
(2)该商品计划最多投入18000元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
【答案】(1)y=![]() 60x+28000;(2)至少要购进100件甲商品,商场可获得的最大利润是22000元
60x+28000;(2)至少要购进100件甲商品,商场可获得的最大利润是22000元
【解析】
(1)根据总利润=(甲的售价-甲的进价)×购进甲的数量+(乙的售价-乙的进价)×购进乙的数量代入列关系式,并化简;
(2)根据总成本≤18000列不等式即可求出x的取值,再根据函数的增减性确定其最值问题;
解:(1)根据题意得:y=(160![]() 80)x+(240
80)x+(240![]() 100)(200
100)(200![]() x),
x),
即:y= ![]() 60x+28000,
60x+28000,
则y与x的函数关系式为:y=![]() 60x+28000;
60x+28000;
(2)80x+100(200![]() x)≤18000,
x)≤18000,
解得:x≥100,
∴至少要购进100件甲商品,
y=![]() 60x+28000,
60x+28000,
∵![]() 60<0,
60<0,
∴y随x的增大而减小,
∴当x=100时,y有最大值,
y大=![]() 60×100+28000=22000,
60×100+28000=22000,
∴若售完这些商品,则商场可获得的最大利润是22000元


科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() x2y-2xy+y2)(-4xy);
x2y-2xy+y2)(-4xy);
(2)6mn2(2-![]() mn4)+(-
mn4)+(-![]() mn3)2;
mn3)2;
(3)-4x2·(![]() xy-y2)-3x·(xy2-2x2y);
xy-y2)-3x·(xy2-2x2y);
(4)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△MNP的三边分别向两边延长,并在每两条延长线上任取两点连接起来,又得到了三个新的三角形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则满足下列条件但不是直角三角形的是( )
A.a2-c2=b2B.a=n2-1, b=2n, c=n2+1 ( n>1)
C.∠A:∠B:∠C = 3:4:5D.∠A=∠B =![]() ∠C
∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:

(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
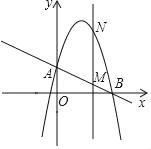
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com