
����Ŀ��ijУ��չУ������ϵ�л����С�������峬�й������ɸ��ľߴ���Ϊ��Ʒ�������ľߴ����ÿ��10Ԫ���������Ķ�����ʱ�ϰ���С���ĶԻ���

��1��������˵ĶԻ����ݣ���С��ԭ�ƻ������ľߴ����ٸ���
��2��ѧУ�������ٴι���ֱʺ�ǩ�ֱʹ�50֧��Ϊ���佱Ʒ�����ι���Ʒ��֧��������400Ԫ�����иֱʱ��ÿ֧8Ԫ��ǩ�ֱʱ��ÿ֧6Ԫ��������ͨ������ϰ����8���Żݣ���ôС�����ɹ���ֱʶ���֧��
���𰸡���1��17����2��100.
��������
����������С��ԭ�ƻ������ľߴ�![]() ������ʵ�ʹ�����
������ʵ�ʹ�����![]() ��������з���
��������з���![]() �����x��ֵ���ɽ��.
�����x��ֵ���ɽ��.
��������С���ɹ���ֱ�![]() ֧������ǩ�ֱ�
֧������ǩ�ֱ�![]() ֧������в���ʽ
֧������в���ʽ![]() �������
�������![]() ���������Թ���100֧.
���������Թ���100֧.
�⣺��1����С��ԭ�ƻ������ľߴ�![]() ������ʵ�ʹ�����
������ʵ�ʹ�����![]() ����
����
������ã�![]() ��
��
���![]() ��
��
��С��ԭ�ƻ������ľߴ�17����
��2����С���ɹ���ֱ�![]() ֧������ǩ�ֱ�
֧������ǩ�ֱ�![]() ֧��
֧��
������ã�![]() ��
��
���![]() ��
��
��![]() ��
��
�������ɹ���ֱ�100֧��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ������1��������n�������²�����
�� ��n���Ϊ����������a��b�ĺͣ�������˻�a��b
�� ����������a��b�ֱ��ظ��˲������õ����������˻�
�� �ظ��������̣�ֱ�������ٲ��Ϊֹ������ֵ�������1��
��n��6ʱ�����еij˻��ĺ�Ϊ_________����n��100ʱ�����еij˻��ĺ�Ϊ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
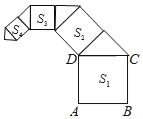
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����������ΪS1����CDΪб��������ֱ�������Σ��Ըõ���ֱ�������ε�һ��ֱ�DZ�Ϊ�������������Σ���������ΪS2���������մ˹��ɼ�����ȥ����S2018��ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�ͬʱ�����ס���������Ʒ��200��������ۺ��ۼ������
��Ʒ���� | �� | �� |
���ۣ�Ԫ/���� | 80 | 100 |
�ۼۣ�Ԫ/���� | 160 | 240 |
�����м�����Ʒ����x�������̳�������200����Ʒ��������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��
��2������Ʒ�ƻ����Ͷ��18000Ԫ���ڹ�����������Ʒ��������Ҫ�������ټ�����Ʒ����������Щ��Ʒ�����̳��ɻ�õ���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
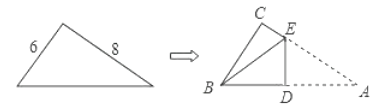
����Ŀ����ͼ��ֱ��������ֽƬ����ֱ�DZ߳��ֱ�Ϊ6.8������ͼ�����۵���ʹ��A���B�غϣ��ۺ�ΪDE�����BDE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=![]() ���Ҿ����㣨2��0����������˵������abc��0����a+b=0����a��b+c=0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��
���Ҿ����㣨2��0����������˵������abc��0����a+b=0����a��b+c=0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��

A���٢ڢۢ� B���ۢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ���ε�ij���й���A��B������Ʒ�����н���һ�������ۿ۵ģ��������������ѽ�����±���
��� ���� | ����A��Ʒ���������� | ����B��Ʒ���������� | ���ѽ�Ԫ�� |
��һ�� | 4 | 5 | 320 |
�ڶ��� | 2 | 6 | 300 |
������ | 5 | 7 | 258 |
����������⣺
��1���������ι������ۿۣ�
��2����A��B������Ʒ��ԭ�ۣ�
��3��������A��B������Ʒ���ۿ�����ͬ�����ۿ�����
��4��С��ͬѧ�ٴι���A��B������Ʒ��10�����ڣ�3�����ۿ�����ǰ���£����ѽ�����200Ԫ�������ٹ���A��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ֽ���ʽ����1��2x2+2xy��3x��3y����2��a2��b2+4a��4b
������̽������ij��ѧ��̽��ѧϰ��С���������ʽ�ֽ���Ŀ����������̽����
̽��1���ֽ���ʽ����1��2x2+2xy��3x��3y
�ö���ʽ����ֱ��ʹ����ȡ����ʽ������ʽ��������ʽ�ֽ⣮������ϸ�۲����ʽ���ص㣮���ָö���ʽǰ�����й���ʽ2x���������й���ʽ��3���ֱ�������������ʣ�µ�����ͬ��ʽ��x+y�������Լ������ṫ��ʽ���ֽ⣮
�⣺2x2+2xy��3x��3y����2x2+2xy������3x+3y����2x��x+y����3��x+y������x+y����2x��3��
�����ҷ��ָö���ʽ�ĵڶ���͵�����й���ʽy����һ��͵�����й���ʽx����y��x�������ʣ�µ�����ͬ��ʽ��2x��3�������Լ������ṫ��ʽ���ֽ⣮
�⣺2x2+2xy��3x��3y����2x2��3x��+��2xy��3y����x��2x��3��+y��2x��3������2x��3����x+y��
̽��2���ֽ���ʽ����2��a2��b2+4a��4b
�ö���ʽ���ֱ��ʹ����ȡ����ʽ������ʽ��������ʽ�ֽ⣬�����������ⰴ̽��1�ķ������飬������a�������һ�鼴a2+4a��a��a+4��������b����һ�鼴��b2��4b����b��b+4����������a��a+4���멁b��b+4����û�й���ʽ���ᣬ���ٷֽ���ȥ����������ϸ�۲췢�֣����Ƚ�a2��b2����һ��Ӧ��ƽ���ʽ�����������һ�飬�������ʽ4����ɼ����������ʽ���Ӷ��ﵽ�ֽ���ʽ��Ŀ�ģ�
�⣺a2��b2+4a��4b����a2��b2��+��4a��4b������a+b����a��b��+4��a��b������a��b����4+a+b��
�������ܽᣩ���Բ���ֱ��ʹ����ȡ����ʽ������ʽ�����зֽ���ʽ�Ķ���ʽ�����ǿɿ��ǰѱ��ֽ�Ķ���ʽ�ֳ������飬�ֱ𰴡���������������ȡ����ʽ�������ù�ʽ�����зֽ⣬Ȼ���ۺ��������ٴ������ϰ��������������������зֽ⣬ֱ���ֽ������������ַֽ���ʽ�ķ�����������ֽⷨ��
����ֽⷨ������һ�ֶ�������ʽ�ֽ�ķ���������ͨ���Զ���ʽ�����ʵ��ķ��飬�Ѷ���ʽת��Ϊ����Ӧ�á������������ֽ�Ľṹ��ʽ��ʹ֮���й���ʽ�����߷��Ϲ�ʽ���ص�ȣ��Ӷ��ﵽ�������á��������������зֽ���ʽ��Ŀ�ģ�
��ѧ�����ã����������÷���ֽⷨ����������⣺
��1���ֽ���ʽ��![]()
��2���ֽ���ʽ��![]()
����չ��������
��3��������������˼·�ֽ���ʽ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
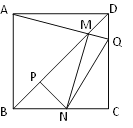
����Ŀ����ͼ���߳�һ����������ABCD��Q��CD��һ���㣬AQ��BD�ڵ�M����M��MN��AQ��BC��N�㣬��NP��BD�ڵ�P������NQ�����н��ۣ���AM=MN��
��MP=![]() BD����BN+DQ=NQ����
BD����BN+DQ=NQ����![]() Ϊ��ֵ������һ����������_______.
Ϊ��ֵ������һ����������_______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com