
����Ŀ��С��ͬѧ���ε�ij���й���A��B������Ʒ�����н���һ�������ۿ۵ģ��������������ѽ�����±���
��� ���� | ����A��Ʒ���������� | ����B��Ʒ���������� | ���ѽ�Ԫ�� |
��һ�� | 4 | 5 | 320 |
�ڶ��� | 2 | 6 | 300 |
������ | 5 | 7 | 258 |
����������⣺
��1���������ι������ۿۣ�
��2����A��B������Ʒ��ԭ�ۣ�
��3��������A��B������Ʒ���ۿ�����ͬ�����ۿ�����
��4��С��ͬѧ�ٴι���A��B������Ʒ��10�����ڣ�3�����ۿ�����ǰ���£����ѽ�����200Ԫ�������ٹ���A��Ʒ���ټ���
���𰸡���1���� ��2��A��30Ԫ/����B��40Ԫ/�� ��3��6 ��4��7��
��������
��1���ɵ����ι����A��B������Ʒ����ͷ���ζ࣬�ܼ۷����٣��ɵó������ι������ۿۣ�
��2����A��Ʒ��ԭ��ΪxԪ/����B��Ʒ��ԭ��ΪyԪ/���������ܼ�=���ۡ��������ǰ���ι�����������ܼۣ����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��3�����ۿ���Ϊz�������ܼ�=���ۡ����������ɵó�����z��һԪһ�η��̣���֮���ɵó����ۣ�
��4���蹺��A��Ʒm��������B��Ʒ��10��m�����������ܼ�=���ۡ�����������ѽ�����200Ԫ�����ɵó�����m��һԪһ�β���ʽ����֮ȡ���е���С�������ɵó����ۣ�
��1���۲�������ݣ���֪�������ι����A��B������Ʒ����ͷ���ζ࣬�ܼ۷����٣�������ι������ۿۣ�
�ʴ�Ϊ������
��2����A��Ʒ��ԭ��ΪxԪ/����B��Ʒ��ԭ��ΪyԪ/������������ã�
![]()
��ã�![]() ��
��
��A��Ʒ��ԭ��Ϊ30Ԫ/����B��Ʒ��ԭ��Ϊ40Ԫ/����
��3�����ۿ���Ϊz����������ã�
5��30![]() 7��40
7��40![]() 258
258
��ã�z=6��
���ۿ���Ϊ6��
��4���蹺��A��Ʒm��������B��Ʒ��10��m��������������ã�
30![]() m+40
m+40![]() ��10��m����200
��10��m����200
��ã�m![]() ��
��
��mΪ��������m����СֵΪ7��
�����ٹ���A��Ʒ7����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=��B=90����E��AB�ϵ�һ�㣬��AE=BC����1=��2��

��1��Rt��ADE��Rt��BECȫ���𣿲�˵�����ɣ�
��2����CDE�Dz���ֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������Ϊ�˱�����̬�������ƻ�����A��B�����ͺŵĻ����豸����֪����һ��A���豸������B���豸����230��Ԫ����������A���豸������B���豸����340��Ԫ��
��1����A���豸��B���豸�ĵ��۸��Ƕ�����Ԫ��
��2��������Ҫ�������Ųɹ�A�ͺ�B���豸��50�ף�Ԥ���ʽ���3000��Ԫ�������ɹ���A���豸�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չУ������ϵ�л����С�������峬�й������ɸ��ľߴ���Ϊ��Ʒ�������ľߴ����ÿ��10Ԫ���������Ķ�����ʱ�ϰ���С���ĶԻ���

��1��������˵ĶԻ����ݣ���С��ԭ�ƻ������ľߴ����ٸ���
��2��ѧУ�������ٴι���ֱʺ�ǩ�ֱʹ�50֧��Ϊ���佱Ʒ�����ι���Ʒ��֧��������400Ԫ�����иֱʱ��ÿ֧8Ԫ��ǩ�ֱʱ��ÿ֧6Ԫ��������ͨ������ϰ����8���Żݣ���ôС�����ɹ���ֱʶ���֧��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻС�����������ϵ�ij��P0������һ�δ�P0��������1����λ��P1�����ڶ��δ�P1������2����λ��P2���������δ�P2������3����λ��P3�������Ĵδ�P3������4����λ��P4��������С�����Ϲ������ˣ�2n+3����ʱ�������������ϵĵ�P2n+3������ʾ����ǡ����n-3������ֻС��ij�ʼλ�õ�P0����ʾ�����ǣ� ��
A.-5B.2C.��1D.-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У���֪AD =8���۵�ֽƬʹAB����Խ���AC
�غϣ���B���ڵ�F�����ۺ�ΪAE����EF=3����AB�ij�Ϊ( )

A. 3 B. 4
C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,DΪ����Rt��ABC��б��AB���е�,EΪBC����һ��,����ED���ӳ���CA���ӳ����ڵ�F,��D��DH��EF��AC��G����BC���ӳ�����H,�����½���:��DE=DG;��BE=CG;��DF=DB;(��BH=CF.������ȷ����____

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƽ��θģ�����ʦ�Ѱ༶��60��ѧ���ֳ�����С�飬ÿС��ֻ����5�˻�6�ˣ����м��ַ��鷽����������
A. 4B. 3C. 2D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���BAC=2��C����BAC��ƽ����AE����ABC��ƽ����BD�ཻ�ڵ�F��FG��AC������DG��
��1����֤��BFBC=ABBD��
��2����֤���ı���ADGF�����Σ�
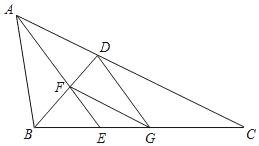
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com