练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G、交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DB;(④BH=CF.其中正确的是____

    【答案】①②③④

    【解析】

    连接CD.欲证线段相等,就证它们所在的三角形全等.证明△DBE≌△DCG,△DCH≌△DAF

    根据已知条件,

    ∵△ABC是等腰直角三角形,CD是中线。

    ∴BD=DC、∠B=∠DCA=45°.

    又∵∠BDC=∠EDH=90°,即

    ∠BDE+∠EDC=∠EDC+∠CDH

    ∴∠BDE=∠CDH

    ∴△DBE≌△DCG(ASA)

    ∴DE=DG BE=CG

    同理可证:△DCH≌△DAF,可得:DF=DH;AF= CH

    ∵BC=AC, CH=AF

    ∴BH=CF

    故答案为①②③④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】完成下列推理证明．

    已知：如图，AD∥EF，∠1＝∠2.

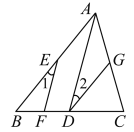
    求证：AB∥DG.

    证明：∵AD∥EF(________)，

    ∴∠1＝∠(_____)（________________）

    ∵∠1＝∠2(已知)，

    ∴∠________＝∠2(________________________)．

    ∴AB∥DG(______________________________________)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直角三角形纸片的两直角边长分别为6.8，按如图那样折叠，使点A与点B重合，折痕为DE，求△BDE的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学三次到某超市购买A、B两种商品，其中仅有一次是有折扣的，购买数量及消费金额如下表：

    类别

    次数

    购买A商品数量（件）

    购买B商品数量（件）

    消费金额（元）

    第一次

    4

    5

    320

    第二次

    2

    6

    300

    第三次

    5

    7

    258

    解答下列问题：

    （1）第　　次购买有折扣；

    （2）求A、B两种商品的原价；

    （3）若购买A、B两种商品的折扣数相同，求折扣数；

    （4）小明同学再次购买A、B两种商品共10件，在（3）中折扣数的前提下，消费金额不超过200元，求至少购买A商品多少件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

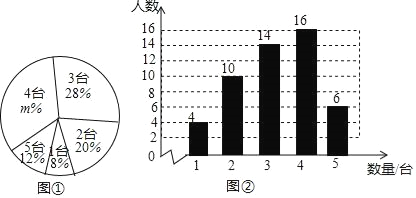
    【题目】随着移动计算技术和无线网络的快速发展，移动学习方式越来越引起人们的关注，某校计划将这种学习方式应用到教育学中，从全校1500名学生中随机抽取了部分学生，对其家庭中拥有的移动设备的情况进行调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

    （1）本次接受随机抽样调查的学生人数为　 　，图①中m的值为　 　；

    （2）求本次调查获取的样本数据的众数、中位数和平均数；

    （3）根据样本数据，估计该校1500名学生家庭中拥有3台移动设备的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）：分解因式：（1）2x2+2xy﹣3x﹣3y；（2）a2﹣b2+4a﹣4b

    （问题探究）：某数学“探究学习”小组对以上因式分解题目进行了如下探究：

    探究1：分解因式：（1）2x2+2xy﹣3x﹣3y

    该多项式不能直接使用提取公因式法，公式法进行因式分解．于是仔细观察多项式的特点．甲发现该多项式前两项有公因式2x，后两项有公因式﹣3，分别把它们提出来，剩下的是相同因式（x+y），可以继续用提公因式法分解．

    解：2x2+2xy﹣3x﹣3y＝（2x2+2xy）﹣（3x+3y）＝2x（x+y）﹣3（x+y）＝（x+y）（2x﹣3）

    另：乙发现该多项式的第二项和第四项含有公因式y，第一项和第三项含有公因式x，把y、x提出来，剩下的是相同因式（2x﹣3），可以继续用提公因式法分解．

    解：2x2+2xy﹣3x﹣3y＝（2x2﹣3x）+（2xy﹣3y）＝x（2x﹣3）+y（2x﹣3）＝（2x﹣3）（x+y）

    探究2：分解因式：（2）a2﹣b2+4a﹣4b

    该多项式亦不能直接使用提取公因式法，公式法进行因式分解，于是若将此题按探究1的方法分组，将含有a的项分在一组即a2+4a＝a（a+4），含有b的项一组即﹣b2﹣4b＝﹣b（b+4），但发现a（a+4）与﹣b（b+4）再没有公因式可提，无法再分解下去．于是再仔细观察发现，若先将a2﹣b2看作一组应用平方差公式，其余两项看作一组，提出公因式4，则可继续再提出因式，从而达到分解因式的目的．

    解：a2﹣b2+4a﹣4b＝（a2﹣b2）+（4a﹣4b）＝（a+b）（a﹣b）+4（a﹣b）＝（a﹣b）（4+a+b）

    （方法总结）：对不能直接使用提取公因式法，公式法进行分解因式的多项式，我们可考虑把被分解的多项式分成若干组，分别按“基本方法”即提取公因式法和运用公式法进行分解，然后，综合起来，再从总体上按“基本方法”继续进行分解，直到分解出最后结果．这种分解因式的方法叫做分组分解法．

    分组分解法并不是一种独立的因式分解的方法，而是通过对多项式进行适当的分组，把多项式转化为可以应用“基本方法”分解的结构形式，使之具有公因式，或者符合公式的特点等，从而达到可以利用“基本方法”进行分解因式的目的．

    （学以致用）：尝试运用分组分解法解答下列问题：

    （1）分解因式：

    （2）分解因式：

    （拓展提升）：

    （3）尝试运用以上思路分解因式：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A、B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：

    种植户

    种植A类蔬菜面积

    （单位：亩）

    种植B类蔬菜面积

    （单位：亩）

    总收入

    （单位：元）

    甲

    3

    1

    12500

    乙

    2

    3

    16500

    说明：不同种植户种植的同类蔬菜每亩平均收入相等．

    （1）求A、B两类蔬菜每亩平均收入各是多少元？

    （2）某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

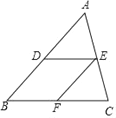
    【题目】如图，在△ABC中，D是AB中点，E是AC中点，F是BC中点，请填空：

    （1）四边形BDEF是　 　四边形；

    （2）若四边形BDEF是菱形，则△ABC满足的条件是　 　．

    （3）若四边形BDEF是矩形，则△ABC满足的条件是　 　．

    （4）若四边形BDEF是正方形，则△ABC满足的条件是　 　．

    并就（2）、（3）、（4）中选取一个进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物，计划同时租用A型车a辆和B型车b辆,一次运完，且每辆车都满载货物.根据以上信息解答下列问题：

    （1）1辆A型车和1辆B型车载满货物一次分别可运货物多少吨？

    （2）请帮助物流公司设计租车方案

    （3）若A型车每辆车租金每次100元，B型车每辆车租金每次120元.请选出最省钱的租车方案，并求出最少的租车费.

    查看答案和解析>>

    同步练习册答案