
【题目】完成下列推理证明.
已知:如图,AD∥EF,∠1=∠2.
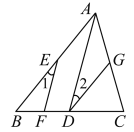
求证:AB∥DG.
证明:∵AD∥EF(________),
∴∠1=∠(_____)(________________)
∵∠1=∠2(已知),
∴∠________=∠2(________________________).
∴AB∥DG(______________________________________)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A、B两种型号的健身器材时,共有多少种组装方案?
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△MNP的三边分别向两边延长,并在每两条延长线上任取两点连接起来,又得到了三个新的三角形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月7日,第十一届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪启动.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项中,错误的是( )
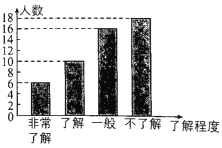
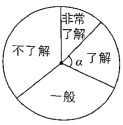
A.抽取的学生人数为50B.“非常了解”的人数占抽取的学生人数的12%
C.![]() D.全校“不了解”的人数估计有428人
D.全校“不了解”的人数估计有428人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G、交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DB;(④BH=CF.其中正确的是____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com