
【题目】健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A、B两种型号的健身器材时,共有多少种组装方案?
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?
【答案】(1)组装A、B两种型号的健身器材共有9种组装方案;(2)总组装费用最少的组装方案:组装A型器材22套,组装B型器材18套
【解析】
(1)设公司组装A型器材x套,则组装B型器材(40-x)套,依题意得![]() ,解不等式组可得;(2)总的组装费用:y=20x+18(40-x)=2x+720,可分析出最值.
,解不等式组可得;(2)总的组装费用:y=20x+18(40-x)=2x+720,可分析出最值.
解:(1)设公司组装A型器材x套,则组装B型器材(40-x)套,依题意得
![]()
解得:22≤x≤30
由于x为整数,∴x取22,23,24,25,26,27,28,29,30
∴组装A、B两种型号的健身器材共有9种组装方案
(2)总的组装费用:y=20x+18(40-x)=2x+720
∵k=2>0,∴y随x的增大而增大
∴当x=22时,总的组装费用最少,最少组装费用是2×22+720=764元
总组装费用最少的组装方案:组装A型器材22套,组装B型器材18套


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,0为坐标原点,点A的坐标为(-4,0),直线BC经过点B(-4,3),C(0,3),将四边形OABC绕点O按顺时针方向旋转α度(0<α≤l80°)得到四边形OA′B′C′,此时直线OA′、直线B′C′,分别与直线BC相交于P,Q.在四边形OABC旋转过程中,若BP=![]() BQ 则点P的坐标为__________.
BQ 则点P的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个动点从点A开始上下来回运动5次,规定向上为正,向下为负。那么这5次运动结果记录如下(单位cm):-5,+7,-3.-11,+3
(1)这个动点停止运动时距离点A多远?在点A的什么位置处?
(2)若这个动点运动速度是2cm/s,运动5次一共需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一套房子的平面图,尺寸如图.
![]() 这套房子的总面积是多少?
这套房子的总面积是多少? ![]() 用含有x、y的代数式表示
用含有x、y的代数式表示![]() .
.
![]() 如果
如果![]() 米,
米, ![]() 米,那么房子的面积是多少平方米?如果每平方米房价为
米,那么房子的面积是多少平方米?如果每平方米房价为![]() 万元,那么房屋总价多少万元?
万元,那么房屋总价多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
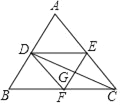
【题目】如图,△ABC中,∠ACB的平分线交AB于点D,作CD的垂直平分线,分别交AC、DC、BC于点E、G、F,连接DE、DF.
(1)求证:四边形DFCE是菱形;
(2)若∠ABC=60,∠ACB=45°,BD=2,试求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:0,-3.14,-(-10),![]() ,-4
,-4![]() ,15%,
,15%,![]() ,0.3,
,0.3,![]() ,10.01001000100001…
,10.01001000100001…
非负整数集合:{ …}
正分数集合:{ …}
无理数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com