
【题目】为推进课改,王老师把班级里60名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( )
A. 4B. 3C. 2D. 1
【答案】B
【解析】
根据题意设5人一组的有x个,6人一组的有y个,利用把班级里60名学生分成若干小组,进而得出等式求出即可.
解:设5人一组的有x个,6人一组的有y个,根据题意可得:
5x+6y=60,y=![]() ,
,
当x=0,y=6符合题意,
当x=1,则y=![]() (不合题意);
(不合题意);
当x=2,则y=![]() ;(不合题意);
;(不合题意);
当x=3,则y=![]() (不合题意);
(不合题意);
当x=4,则y=![]() (不合题意);
(不合题意);
当x=5,则y=![]() (不合题意);
(不合题意);
当x=6,则y=5
当x=7,则y=![]() (不合题意);
(不合题意);
当x=8,则y=![]() (不合题意);
(不合题意);
当x=9,则y=![]() (不合题意);
(不合题意);
当x=10,则y=![]() (不合题意);
(不合题意);
当x=11,则y=![]() (不合题意);
(不合题意);
当x=12,则y=0
故有3种分组方案.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.

(1)画出△A1OB1;
(2)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
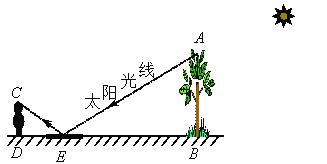
【题目】为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度(精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-1、2、-4、8、-16、32、-64、……①
0、3、-3、9、-15、33、-63、……②
1、-5、7、-17、31、-65、127、……③
(1) 第①行的第8个数是___________,第①行第n个数是___________(用n的式子表示)
(2) 取第①、②、③行的第10个数分别记为a、b、c,求a-b+c的值
(3) 取每行数的第n个数,这三个数中任意两数之差的最大值为6146,则n=__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com