
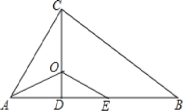
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△AOE;
(2)求证:OE∥BC。
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
![]()
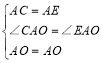 ,
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则满足下列条件但不是直角三角形的是( )
A.a2-c2=b2B.a=n2-1, b=2n, c=n2+1 ( n>1)
C.∠A:∠B:∠C = 3:4:5D.∠A=∠B =![]() ∠C
∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,点D是BC边上一点,以AD为直径的⊙O与BC相切于点D,与AD、AC分别交于点E、F.
(1)如图①,若∠AEF=52°,求∠C的度数.
(2)如图②,若EF经过点O,且∠AEF=35°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
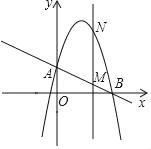
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
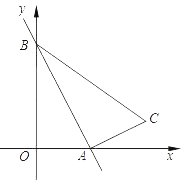
【题目】已知一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC=90°,tan∠ABC=![]() .
.
(1)求点C的坐标;
(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得2S△ABM=S△ABC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com