
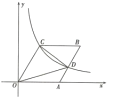
【题目】如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数![]() 的图象与AB交于点D,则△COD的面积为( )
的图象与AB交于点D,则△COD的面积为( )
A.![]() B.
B.![]() C.4D.
C.4D.![]()
【答案】B
【解析】
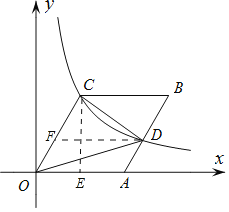
易证S菱形ABCO=2S△CDO,再根据tan∠AOC的值即可求得菱形的边长,即可求得点C的坐标,可得菱形的面积和结论.
解:作DF∥AO,CE⊥AO,
∵∠AOC=60°,
∴tan∠AOC=![]() ,
,
∴设OE=x,CE=![]() x,
x,
∴x![]() x=4
x=4![]() ,
,
∴x=±2,
∴OE=2,CE=2![]() ,
,
由勾股定理得:OC=4,
∴S菱形OABC=OACE=4×2![]() =8
=8![]() ,
,
∵四边形OABC为菱形,
∴AB∥CO,AO∥BC,
∵DF∥AO,
∴S△ADO=S△DFO,
同理S△BCD=S△CDF,
∵S菱形ABCO=S△ADO+S△DFO+S△BCD+S△CDF,
∴S菱形ABCO=2(S△DFO+S△CDF)=2S△CDO=8![]() ,
,
∴S△CDO=4![]() ;
;
故选:B.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
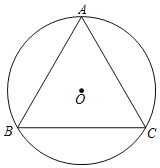
【题目】如图,等边△ABC,作它的外接圆⊙O,连接AO并延长交⊙O于点D,交BC于点E,过点D作DF∥BC,交AC的延长线于点F.
(1)依题意补全图形并证明:DF与⊙O相切;
(2)若AB=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
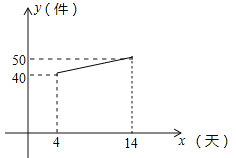
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 号楼在
号楼在![]() 号楼的南侧,两楼高度均为
号楼的南侧,两楼高度均为![]() 楼间距为
楼间距为![]() .冬至日正午,太阳光线与水平面所成的角为
.冬至日正午,太阳光线与水平面所成的角为![]() .
.![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() ,春分日正午,太阳光线与水平面所成的角为
,春分日正午,太阳光线与水平面所成的角为![]() ,
,![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() .已知
.已知![]() .
.
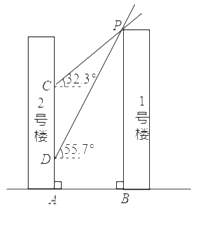
(1)求楼间距![]() ;
;
(2)若![]() 号楼共
号楼共![]() 层,层高均为
层,层高均为![]() 则点
则点![]() 位于第几层? ( 参考数据:
位于第几层? ( 参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,市场上防护口罩出现热销.某药店用![]() 元购进甲,乙两种不同型号的口罩共
元购进甲,乙两种不同型号的口罩共![]() 个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的
个进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的![]() 倍.
倍.
![]() 求购进的甲,乙两种口罩的单价各是多少?
求购进的甲,乙两种口罩的单价各是多少?
![]() 若甲,乙两种口罩的进价不变,该药店计划用不超过
若甲,乙两种口罩的进价不变,该药店计划用不超过![]() 元的资金再次购进甲,乙两种口罩共
元的资金再次购进甲,乙两种口罩共![]() 个,求甲种口罩最多能购进多少个?
个,求甲种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
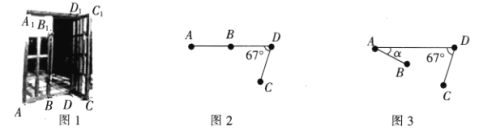
(1)求点C到AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com