
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
【答案】(1)不是,理由见详解;(2)是,当35°≤∠A≤40°时,△ABC为“差角三角形”, 且∠A是∠B的“差角”; 当50°≤∠B≤70°时,△ABC为“差角三角形”, 且∠B是∠C的“差角”.
【解析】
(1)根据差角定义即可判断;
(2)根据∠B的度数范围求出∠A的度数范围,再分别讨论两个角之间是“差角”时的取值范围,如果符合取值范围即是“差角”,否则即不是.
(1)△ABC不是“差角三角形”,理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60![]() ,
,
∴∠A=![]() ∠B+30
∠B+30![]() ,
,
∵![]() ,
,
∴△ABC不是“差角三角形”;
(2)∵∠C=90°,
∴∠A+∠B=90°,
∵50°≤∠B≤70°,
∴20°≤∠A≤40°,
①∠B是 ∠A的“差角”时,∠B=![]() ∠A+α,
∠A+α,
∵![]() ,
,
∴10![]() 45
45![]() ,
,
不满足题意,舍去;
②∠A是∠B的“差角”时,∠A=![]() ∠B+α,
∠B+α,
∵![]() ,
,
∴25![]() 60
60![]() ,
,
∵20°≤∠A≤40°,
∴25°≤∠A≤40°,
当∠A=![]() ∠B时,∠A=35°,
∠B时,∠A=35°,
∴当35°≤∠A≤40°时,△ABC为“差角三角形”, 且∠A是∠B的“差角”.
③∠C是∠B的“差角”时,∠C=![]() ∠B+α,
∠B+α,![]() ,
,
∴25![]() ,不满足题意,舍去;
,不满足题意,舍去;
④∠B是 ∠C的“差角”时,∠B=![]() ∠C+α,
∠C+α,![]() ,
,
∴45![]()
∴当50°≤∠B≤70°时,△ABC为“差角三角形”, 且∠B是∠C的“差角”.
⑤∠A是∠C的“差角”时,∠A=![]() ∠C+α,
∠C+α,![]() ,
,
∴45![]() ,不满足题意,舍去;
,不满足题意,舍去;
⑥∠C是∠A的“差角”时,∠C=![]() ∠A+α,
∠A+α,![]() ,
,
∴10![]() ,不满足题意,舍去;
,不满足题意,舍去;
综上,当35°≤∠A≤40°时,△ABC为“差角三角形”, 且∠A是∠B的“差角”; 当50°≤∠B≤70°时,△ABC为“差角三角形”, 且∠B是∠C的“差角”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=6![]() ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4),(1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°—∠ABC—2x°,则下列角中,大小为x°的角是

A.∠EFCB.∠ABCC.∠FDCD.∠DFC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形OACB为长方形,A(﹣6,0),B(0,4),直线l为函数y=﹣2x﹣5的图象.
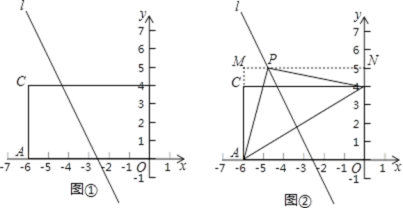
(1)点C的坐标为 ;
(2)若点P在直线l上,△APB为等腰直角三角形,∠APB=90°,求点P的坐标;
小明的思考过程如下:
第一步:添加辅助线,如图②,过点P作MN∥x轴,与y轴交于点N,与AC的延长线交于点M;
第二步:证明△MPA≌△NBP;
第三步:设NB=m,列出关于m的方程,进而求得点P的坐标.
请你根据小明的思考过程,写出第二步和第三步的完整解答过程;
(3)若点P在直线l上,点Q在线段AC上(不与点A重合),△QPB为等腰直角三角形,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察发现:如图(1),![]() 是
是![]() 的外接圆,点
的外接圆,点![]() 是边
是边![]() 上的一点,且
上的一点,且![]() 是等边三角形.
是等边三角形.![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为圆心、
为圆心、![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)![]() _____;
_____;
(2)线段![]() 、
、![]() 有何大小关系?证明你的猜想.
有何大小关系?证明你的猜想.
拓展应用:如图(2),![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 延长线上的一点.点
延长线上的一点.点![]() 是
是![]() 的外接圆圆心,
的外接圆圆心,![]() 与
与![]() 相交于点
相交于点![]() .如果等边三角形
.如果等边三角形![]() 的边长为2,请直接写出
的边长为2,请直接写出![]() 的最小值和此时
的最小值和此时![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com